Group 3 2014
Group members: Andras Karsai, Steven Harrington, and Colin Campbell

We seek to investigate the properties of a generalized double pendulum. Previous investigations on double pendulums often limit it to a planar case, and fix the lengths of each stage of the pendulum. The Astrojax is notable in that the pendulum stage lengths vary dynamically. We measure its behaviors in response to well quantified forcing using a perpendicular camera array to track position, and from that generate three-dimensional trajectories for each pendulum bob. The trajectories' mean chaotic lifetime and dominant oscillation frequencies are analyzed, and we find that this chaotic pendulum's oscillation frequencies are linearly correlated with the forcing frequency in the low-frequency regime. We also conclude that a naive periodic forcing of this system without a feedback mechanism is not sufficient to create stable, long-lived orbits of the Astrojax pendulum.
Introduction
An oscillation <ref>http://en.wikipedia.org/wiki/Oscillation</ref> is defined, in physics, as a regular variation in magnitude, position, etc. around a central point. Oscillatory mechanical systems are a vast subset of dynamical systems. They can be used to describe the evolution of states for nearly all physical phenomena. Oscillations of various types occur in real world mechanical systems, nearly all of which are thermodynamically irreversible (via damping, friction, energy due to heat loss, etc.). Even the light you see and the sound you hear are the results of the oscillations of a medium or a field. Here, we specifically study a set of coupled, chaotic oscillations that form from the forcing of a double pendulum.
As any good physics enthusiast knows, student, instructor, or otherwise, pendula are one of the most fundamental and ubiquitous systems studied, and while they may be common, they are only ideal and easily solvable in the most simple of cases. While the equations of motion for a single pendulum are easily attainable, especially for the low amplitude/small angle limit, a "double" pendulum is an example of the effects of coupling and gives rise to chaotic behavior.
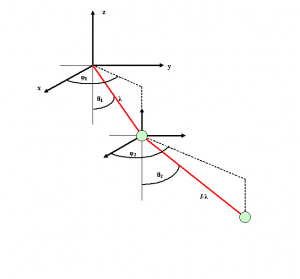
Traditionally, a double pendulum has rigid axes, thereby defining the distance the two masses that can be from each other and also from the pivot. Also, more oft than not, a double pendulum is constrained to move in two dimensions via a constant, fixed polar angle. As such, the system has only two degrees of freedom: <math>\scriptsize{\theta_1}</math> and <math>\scriptsize{\theta_2}</math>, these being the azimuthal angles the axes of their respective masses form with the vertical.
It is well documented that such a system demonstrates chaotic behavior. However, we wish to examine the kinds of behavior that arise when we increase the degrees of freedom from two to five. How does one go about doing this? The answer is found very simply in a child's toy: the Astrojax.
The Astrojax Pendulum
The Astrojax is an assemblage of three weighted spheres on a string. Some versions of the toy allow all three spheres to move along the length of the string, but the case studied here does not. Two of the spheres are located at the ends of the string, and the third sphere is allowed to move along the length of the string between them. Some small amounts of damping are of course present. For the Astrojax, the polar angles are not constrained, allowing for motion in a three dimensional plane. This gives the Astrojax five degrees of freedom:
- <math>\small{\lambda}</math> - The distance between the first and middle sphere
- <math>\small{\theta_1}</math> - The first axis' azimuthal angle
- <math>\small{\theta_2}</math> - The second axis' azimuthal angle
- <math>\small{\phi_1}</math> - The first axis' polar angle
- <math>\small{\phi_2}</math> - The second axis' polar angle
The lengths of the two pendula are defined as <math>\scriptsize{L_1=\lambda}</math> and <math>\scriptsize{L_2 = L- \lambda}</math> where <math>\scriptsize{L_1}</math> and <math>\scriptsize{L_2}</math> are the lengths of the first and second pendula, respectively, and where <math>\scriptsize{L}</math> is the total length of the string. It is important to note that because the length of the string is held constant and the length of the second pendulum depends on length of the first and the total length of the string, the length of the second pendulum is not an additional degree of freedom; it can be obtained through other lengths and variables already inherent in the system.
Hopefully, the addition of these three degrees of freedom will give rise to even more interesting chaotic behavior; if a rigid, double pendulum already possess chaotic properties, surely an unconstrained one will exhibit even more chaos, especially under forcing.
Previous Work
Surprisingly, the dynamics of three dimensional double pendulum are not well studied, not to mention those of a three dimensional variable length pendulum. Most studies of such systems constrain the lengths of the two pendula to be constant, giving them only four degrees of freedom as opposed to five for the Astrojax. Prior work is scarce, but there are some examples by Philip du Toit and Daniel Dichter and Kate Maschan.
The first differs from our experimental approach in that Dr. Du Toit simulated the system as whole. He simulated all three bobs, without any forcing, starting from some initial conditions. While his mathematical approach is still useful, his experimental process offers little in the way of the investigation of chaos, as he merely examined the dynamics of the system starting from some initial conditions, and did not infinitesimally vary those conditions to investigate how much differently the system evolved over time, which is one of the definitions of chaos.
Daniel Dichter and Kate Maschan completed much the same work as our group, however, they considered the string on which the Astrojax bobs were attached/moved to be a spring with some spring constant <math>\scriptsize{k}</math>, and they also took into account all viscous (i.e., damping) forces. Their paper is a qualitative approach to the system in much the same way ours ended up being a qualitative approach.
Methods
The motion of the Astrojax is, by nature, extremely complex. The motion of a double pendulum constrained to move in only two dimensions is already chaotic, and the sheer complexity of allowing motion in three dimensions can easily be extrapolated. It also bears stating that Astrojax is not purely a double pendulum. The center mass is free to move along the string, allowing the length of the two coupled pendulums to vary, but it is, fortunately, constrained to stay on the string itself, between the two end masses.
In order to proprerly observe, quantify, and analyze the data we made use of the Optitrack motion capture system and its proprietary software MOTIVE. A DENSO robotic arm held one of the end masses of the Astrojax and forced it, resulting in oscillations.
We forced the Astrojax in the vertical, or <math>\small{z}</math> direction in a trianglar wave rhythm using various speeds and amplitudes of the robotic arm. The software WINCAPS III was used in order to interface and program the robotic arm. The Astrojax were covered in infrared reflective tape for purposes of motion capture, along with a point on the robot arm. Thus, we could capture the three-dimensional dynamics of the two free bobs along with the forcing trajectories. Once captured and trajectorized, Optitrack's interpretation of marker disappearances and swaps in vertical position resulted in data gaps, marker identity loss, and marker switching. A tracking program in MATLAB was implemented (credit to M. Kingsbury) which used a ternary search algorithm which searched for least position differences in order to resolve each marker into a continuous path. Therefore we could achieve full 3-D trajectories for the middle & end bobs, along with the forcing marker.
In addition, we investigated the forcing motions used by a human in creating stable orbits with the Astrojax. To do this, we attached an infrared reflective marker to the human forcer's hand via a glove, and implemented the same methodology as with the robotic forcing, simply replacing the forcing marker.

Physical Interpretation of the System
Previous analysis of the Lagrangian<ref>http://www.cds.caltech.edu/~marsden/wiki/uploads/projects/geomech/Dutoit2005.pdf</ref> and the Newtonian<ref>http://www.katemaschan.com/uploads/2/4/4/5/24451800/astrojax_final_report.pdf</ref> equations of motion have been derived in previous works. We provide a summary of these equations below. The generalized cooridnates are given as: <math> \scriptsize{q = [x_1,y_1,z_1,x_2,y_2,z_2]} </math>
This allows us to write the Lagrangian of the system as: <math> \scriptsize{L = \frac{1}{2}\dot{q}^TM\dot{q}-V(q)} </math> where <math>\scriptsize{V(q)=g(m_1z_1 + m_2z_2)}</math> and
<math> \scriptsize{M = \begin{bmatrix} m_1 & 0 & 0 & 0 & 0 & 0 \\ 0 & m_1 & 0 & 0 & 0 & 0\\ 0 & 0 & m_1 & 0 & 0 & 0\\ 0 & 0 & 0 & m_2 & 0 & 0\\ 0 & 0 & 0 & 0 & m_2 & 0\\ 0 & 0 & 0 & 0 & 0 & m_2\\ \end{bmatrix}} </math>
The Newtonian form of the system is
- <math>a_{2x} = \frac{Fs_{1x}-Fs_{2x}+Fd_{2x}}{m_2} </math>
- <math>a_{2y} = \frac{Fs_{1y}-Fs_{2y}+Fd_{2y}}{m_2} </math>
- <math>a_{2z} = \frac{Fs_{1z}-Fs_{2z}+Fd_{2z}}{m_2}-g</math>
- <math>a_{3x} = \frac{Fs_{2x}+Fd_{3x}}{m_3}</math>
- <math>a_{3y} = \frac{Fs_{2y}+Fd_{3y}}{m_3}</math>
- <math>a_{3z} = \frac{Fs_{2z}+Fd_{3z}}{m_3}-g</math>
where $\scriptsize{a_{ij}}$ is the acceleration of the $\scriptsize{i^{th}}$ mass in $\scriptsize{j}$ direction, $\scriptsize{g}$ is the acceleration due to gravity $\scriptsize{Fs_{\alpha\beta}}$ is the force of the string on mass $\scriptsize{\alpha}$ in the $\scriptsize{\beta}$ direction, and $\scriptsize{Fd_{\alpha\beta}}$ is the drag force and follows the same conventions as above.
While these equations provide a good interpretation of the Astrojax pendulum with a taut string, we find they do not cover a great deal of cases that occur in the real system we tested. For example, the Newtonian equations do not cover cases where the string goes slack unless the tensile force component is made piecewise active. This piecewise behavior can make the set of ordinary differential equations analytically intractable for traditional analysis methods.
In addition, the real system where Astrojax bobs with a finite radius are physically touching is not accounted for, as the actual degenerate state of the two bobs touching does not have them located at the same position.
Results
All Figures are located in the gallery below
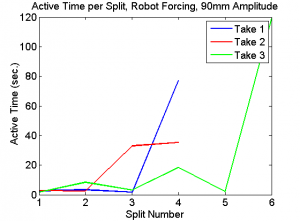
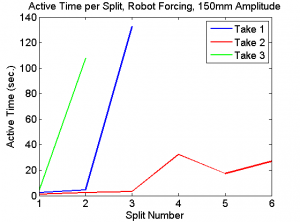
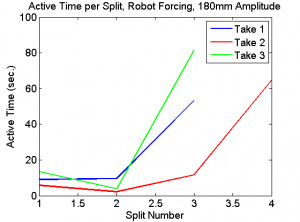
We recorded an average of three takes each for each amplitude of robotic forcing, and five takes each for each type of human forcing (Horizontal, Vertical, Butterfly). In general, the naive method of having the robot arm force the Astrojax with a periodic motion with no feedback did not result in any stable orbits occurring, only quasi-stable and/or chaotic orbits that rapidly change or decay. In the robotic forcing, we found that a sufficient degree of acceleration was required in order to separate the two bobs from one another and cause the system to evolve away from the trivial state (i.e. the two bobs remain in contact with one another at the string's nadir).
Once separated in the robotic forcing, we found the Astrojax did not follow any predictable behaviors; their motion was mostly chaotic under this simple periodic forcing. The duration of time where the bobs were in this chaotic behavior vs. the time they spent in the trivial state increased overall as the forcing progressed, as shown in the plots below.
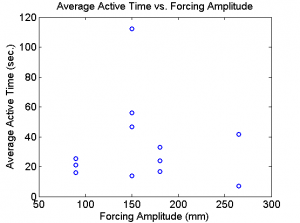
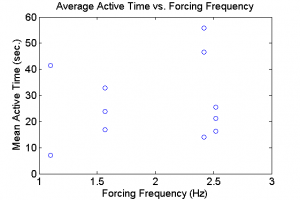
We also plot the mean active time of each take vs. each forcing's respective amplitude and frequency. As seen in Fig. 4, there is high variance in the mean active time solely for a forcing amplitude of 150mm, while the remaining amplitudes cluster around having 30 seconds. Figure 5 shows the same data with respect with the forcing frequency. Note that a small difference in forcing frequency near 2.5 Hertz seemed to generate a wider spread of mean active times.
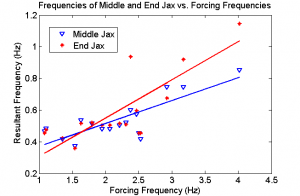
Using MATLAB's Fast Fourier Transform (FFT), we found the most dominant frequency in the recorded oscillations in all three Cartesian dimensions. The resultant frequencies were often symmetrical about the Cartesian $\scriptsize{x}$ & $\scriptsize{y}$ coordinates, while FFTs of the $\scriptsize{z}$ coordinate often failed or were too noisy for some unknown reason. The plot below shows the resultant frequencies of each bob as a function of each take's forcing frequency.
As seen in Fig. 6, as the forcing frequency increases, the resultant dominant oscillation frequency for each bob tends to increase in a roughly linear manner, with the end bob increasing slightly faster than the middle bob.
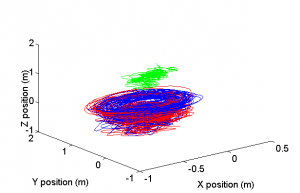
With M. Kingsbury's tracking program, we created full 3-D plots and movies of the tracked trajectories. We provide one of the more interesting plots below: a trajectory plot of human forcing creating a stable horizontal orbit (Fig. 7).
The interesting part of the forcing is the green trajectory created by the human forcing marker. As seen in the plot, a complicated, helical path in order to maintain a steady horizontal orbit. The dynamic path that the human forcing creates with changing frequencies and amplitudes implies that some human 'feedback' mechanism is necessary to create such stable orbits.
Discussion
From our results, we can qualitatively confirm certain aspects of the Astrojax system. As seen in Figure 8, the resultant frequencies of the middle & end bobs increase linearly as the forcing frequency increases. We suspect that at higher forcing frequencies this linear relation will no longer be true as the forcing frequency becomes too fast and the end bobs no longer have time to fall sufficient distances to split.
Figures 1 thru 3 demonstrate that the active time of the end bobs increased as the Astrojax split from each other. These results match our qualitative observations with the robotic forcing. Often what would happen is that the forcing would generate small, short-lived splits of the jax that would either rapidly decay or create small, unstable orbits. It was only after some time of forcing and a few of these small splits that the jax would separate enough to create the full, rich, chaotic orbits with active times in the dozens of seconds.
Another observation we made in our experiments was that under certain smooth motions of the robotic arm's end affector, the Astrojax would not deign to split under any attempted forcing frequency or amplitude. This occurred because the type of motion interpolation used was too smooth, and the robot arm was slowing down before reaching its assigned endpoint. Using a different kind of interpolation generated a much jerkier motion and successful splitting of the Astrojax. Thus, we strongly suspect that a sufficient degree of acceleration is required to separate the bobs, an acceleration which most likely must exceed $\scriptsize{g}$. This acceleration is generated by a sufficiently jerky motion, since acceleration is the antiderivative of jerk.
Conclusion
The Astrojax is a very complex system with a great deal of dynamics and oscillatory patterns, especially when real-world constraints and perturbations are accounted for. From our results, we found that it is not feasible to generate stable orbits of any kind using a simple, naive periodic forcing. The best we could do was to create chaotic orbits that had some mean lifetime before eventually decaying. When examined alongside the complicated motions of human forcing that were necessary to create stable orbits, we conclude that some kind of feedback mechanism is needed to adjust the forcing frequency and/or amplitude on the fly to maintain a stable orbit.
Future work on the Astrojax system could involve creating a 3-D ordinary differential equation solver to simulate the trajectories of the Astrojax under our attempted forcings. We could then compare experimental vs. simulated trajectories and find differences in resultant frequencies and mean active times that arise from real-world constraints. Since we still have the raw data of the forcing trajectories and the initial conditions of the system, it would be simple to input those parameters into a ODE solver like MATLAB's Simulink library and examine differences in resultant trajectories that arise from the nonlinearities and chaos inherent in this system.
Figure Gallery
Experiment Videos and Photos
| <videoflash>qvpj1DxlpX0</videoflash> | <videoflash>KlnBpO_LThE</videoflash> | <videoflash>lGg5QRCDRCs</videoflash> | <videoflash>IeAsMpIIsPw</videoflash> |
| <videoflash>wU8yi3MdGhc</videoflash> | <videoflash>rrZDmMzerEo</videoflash> | <videoflash>_tt-gAX3mq4</videoflash> |