Group 4
Synchronization of metronomes
Group Members: Jeff Tithof, Brad Taylor, Luis Jover, & Vlad Levenfeld
Presentation. Papers: Vlad, Luis, Brad, Jeff
The synchronization of coupled oscillations has proven to be a useful model for describing the dynamics of a large number of physical systems. Perhaps the simplest system which can capture such dynamics is that of two oscillators coupled through the motion of a free platform. In recent years, there has been a considerable amount of research on the case of $N=2$; however, little work has extended to larger numbers of oscillators. The goal of the current work is to quantify the time to synchronization for $N=2$ through $N=9$ metronomes on a movable platform, through experimental investigation and numerical simulation. Our results show a considerable level of agreement between the two, and discrepancies are explored. Possibilites for future work and potential improvements are noted.
Background
The phenomenon of synchronization is found throughout nature and in many applications of different fields of science<ref>Steven H. Strogatz, Nonlinear Dynamics and Chaos, Westview, Cambridge (1994).</ref>. Examples of synchronization include the flashing of firefly populations, the firing of pacemaker cells in the heart, applications of Josephson junctions, coupled fiber laser arrays, and perhaps even epileptic seizures. Many instances of synchronization in nature and applications in science become extremely complicated as soon as multiple variables or several coupled oscillators are introduced. However, the pervasive presence of synchronization in nature and science motivates work towards a deep understanding of such phenomena. So, as with any system that is to be scientifically understood, the simplest case is the best place to begin; for synchronization, the case of two identical, coupled oscillators is perhaps the simplest.
Research into the mutual synchronization of two identical coupled oscillators is believed to date back to the work of Christiaan Huygens in the 1600's, in which he discovered and investigated the synchronization of two pendulum clocks hanging on a common support beam <ref>Huygens C. Œuvres complètes de Christiaan Huygens. vol. 17. The Hague: Martinus Nijhoff; 1932.</ref>. Motivated by the goal of solving the ``Longitude Problem," Huygens reached some insightful conclusions about the nature of this system, eventually concluding that small movements of the support beam with every oscillation were responsible for the antiphase synchronization that consistently occurred.
Significant progress has been made in explaining simple instances of synchronization. In 2002, Bennett et al. <ref>M. Bennett, M. F. Schatz, H. Rockwood, and K. Wiesenfeld, ``Huygens's clocks," Proc. R. Soc. Lond. A 458, 563-579 (2002).</ref> constructed an apparatus meant to recreate the setup described by Christiaan Huygens. The experimental and numerical results agree qualitatively with records from Huygens's research. Concurrently, Pantaleone <ref>J. Pantaleone, ``Synchronization of metronomes," American Journal of Physics 70, 992-1000 (2002).</ref> investigated a similar setup in which metronomes were placed on a common support which was free to roll across cylinders, allowing coupling through the low-friction horizontal translation of the platform. Pantaleone's theoretical analysis provided agrees with the experimental observations reported.
In 2009, Ulrichs et al. <ref>H. Ulrichs, A. Mann, and U. Parlitz, ``Synchronization and chaotic dynamics of coupled mechanical metronomes," Chaos 19, 043120 (2009).</ref> reported agreement with Pantaleone's results in computer simulations. Additionally, these simulations were run for coupling of up to 100 metronomes and reportedly showed chaotic and hyperchaotic behavior. A paper by Wiesenfeld and Borrero-Echeverry <ref>Daniel Borrero-Echeverry and Kurt Wiesenfeld, ``Huygens (and Others) Revisted," Accepted for publication in Chaos, Obtained through personal contact (2011).</ref>, currently in the process of publication, investigates how varying the parameters of two coupled oscillators can affect the synchronization outcome.
An arguably strong theoretical understanding of the $N=2$ case has been developed in recent years; it seems appropriate to expand this theory to a larger number of coupled oscillators. This is the goal of the current work.
Experiment
Phenomenologically, as expected, one observes more complicated dynamics as the number of coupled metronomes increases. Below are two videos, for the cases of $N=2$ and $N=8$, respectively, which demonstrate this. Our experimental goal is to quantify this behavior.
<videoflash>AMwDIIeacvs</videoflash> <videoflash>h1wY13XspVI</videoflash>
Experimental Materials and Methods
The experimental setup for this project is conveniently very simple, but care must be given to reduce external influences that can easily alter the dynamics of non-linear systems.
Our system consists of anywhere from two to nine metronomes, a flat, thick poster-board platform, and two rollers (empty 12 fl. oz diet coke cans). The basic setup is shown to the right, with the metronomes always being placed along a 1-dimensional array.
The metronomes are Wittner’s Super-Mini-Taktell (Series 880). We tested each metronome's capability of synchronizing in the N=2 case. This resulted in us removing a metronome due to anomalous behavior. We tracked the data using a camera set for 42 frames per second that was connected to LabView on a PC. For data collection, we blacked out the pendulum surface and the reflective casing near the pendulum bob. This aided LabView in tracking a single white dot applied with white-out on each metronome bob. Similarly we spray-painted the poster-board platform black and applied a white dot on its side to track the motion. Finally we placed the entire system on a thin, smooth plastic block used to reduce frictional irregularities liable from the table surface.
During our week in the lab we ran 20 usable data-runs for $N={2,3,5,6,7,9}$, 19 data-runs for $N=4$, and 12 runs for $N=8$. The metronomes were set for 200 beats per minute, which corresponds to 100 periods per minute. For each run we set up LabView to track the platform and the metronome bobs. Once the camera was tracking we stabilized the platform by hand as we set the metronomes one-by-one in motion. As the last metronome was set in motion we let go of the platform. We considered this the beginning of the run. The system was allowed to evolve for 90 seconds or longer depending on whether synchronization seemed to occur. For some of the higher N cases synchronization did not occur despite allowing the metronomes to wind completely down.
Experimental Analysis
Our goal was to determine the dependence of time to synchronization on the number of metronomes. We used the raw data output of times and x-positions (from the camera lens’ point of view in pixel units). We considered a strict definition of synchrony where metronomes are in-phase.
Due to camera distortions and small tracking errors, we chose to consider the turning points of the data as opposed to the entire time series. By using the findpeaks function in Matlab our time-series data was reduced to a vector of peak times for each metronome. We chose to look at peaks occurring at only one turning point ensuring our analysis would not falsely detect anti-phase phase-locking as an occurrence of our stricter synchronization.
We developed an algorithm for determining synchrony for use with the experimental data and the simulation data. The peak times will occur at the same time for systems in in-phase synchrony. However for the real data, this is not expected even when synchronization has phenomenologically occurred because of slight noise in the system, errors in tracking, and discretization of time. As a result we cannot discount synchronization from being achieved even if peaks occur at slightly different times for the metronomes. This motivates a time-$\epsilon$ definition of synchronization. We introduce the model parameter $\epsilon_{time}$ where if all metronome peaks occur within it we consider that time an instant of synchrony. Full synchronization occurs when so many instances of synchrony occur in a row (defined by another model parameter, $r$).
After trimming the data of all time before the platform is destabilized and determining the peaks, the output data is reduced to a vector of peak times for each metronome. The size of each vector is not necessarily the same, however any instance of synchrony must contain any elements from each vector so we look for instances of synchrony by arbitrarily choosing one vector and considering its time elements in succession, $v_{arb}$. In order to reduce the arbitrariness we used an algorithm that updated the reference time for placing the $\epsilon_{time}$ ball. Initially we look around the arbitrary metronome peak time. Any peak times from other metronomes within the $\epsilon_{time}$ are placed in a set with the original reference peak time and the average time becomes the new reference for the $\epsilon_{time}$. This procedure is continued until no further peak times are picked up. At this point, if the number of elements is equal to $N$ we consider it a syncing instance and place the reference time in a set, $\mathcal{S}$, and we move to the next peak time in $v_{arb}$. If an instance of syncing does not occur, $\mathcal{S}$ becomes the empty set and we move to the next peak time in $v_{arb}$. When the cardinality of $\mathcal{S}=r$ we take the $min({\mathcal{S}})$ as the time of synchronization, $t_{sync}$ for the run.
Theory & Simulation
Equations of Motion
The equations of motion for two coupled pendulums are available in Bennett et al. and Wiesenfeld and Borrero-Echeverry. These equations may easily be extended to $N$ metronomes:
\begin{equation} \label{dim_eq1} \ddot\phi_j+b\dot\phi_j+\frac{g}{l}\sin\phi_j=-\frac{1}{l}\ddot X \cos\phi_j+F_j \end{equation}
\begin{equation} \label{dim_eq2} (M+m)\ddot X+B\dot X = -ml\frac{d^2}{dt^2}(\sin\phi_1+\sin\phi_2+ ... +\sin\phi_N) \end{equation} where $\phi_j$ is the angular displacement of the jth pendulum, $b$ is the pivot damping coefficient, $g$ is the acceleration due to gravity, $l$ is the pendulum length, $X$ is the linear displacement of the platform, $F$ is the impulsive drive, $M$ is the platform mass, $m$ is the metronome bob mass, $B$ is the platform friction coefficient, and the dots represent differentiation with respect to time.
Nondimensionalizing results in the following:
\begin{equation} \label{nondim_eq1} \frac{d^2\phi_j}{{d\tau}^2}+2\tilde\gamma\frac{d\phi_j}{d\tau}+\sin\phi_j=-\frac{d^2Y}{{d\tau}^2}\cos\phi_j+\tilde F_j \end{equation}
\begin{equation} \label{nondim_eq2} \frac{d^2Y}{{d\tau}^2}+2\Gamma\frac{dY}{d\tau}=-\mu\frac{d^2}{d\tau^2}(\sin\phi_1+...+\sin\phi_N) \end{equation}
where we have introduced the dimensionless parameters:
\begin{equation} \label{nondim_param1} \tau=t\sqrt{\frac{g}{l}} \end{equation}
\begin{equation} \label{nondim_param2} \mu=\frac{m}{M+Nm} \end{equation}
\begin{equation} \label{nondim_param3} \tilde\gamma=b\sqrt{\frac{l}{4g}} \end{equation}
\begin{equation} \label{nondim_param4} \Gamma=\frac{B}{(M+Nm)}\sqrt{\frac{l}{4g}} \end{equation}
All parameters and variables described are well defined and may be experimentally measured, with the exception of $\tilde{F_j}$, the impulsive drive of the metronome, which receives a treatment first described in Bennett et al. The escapement mechanism which ``kicks" the metronome is mimicked in two parts: first, the angular velocity of the pendulum is slowed by some factor $\gamma$, and then, a numerical constant $c$ is added to the angular velocity:
\begin{equation} \label{kick} \left|\frac{d\phi}{d\tau}\right|\to\gamma\left|\frac{d\phi}{d\tau}\right|+c \end{equation}
This nature of the escapement mechanism and the validity of this model is perhaps most visible for very low frequencies, as seen in the following video. Notice the "slow-down-then-kick" behavior of the pendulum around $\phi=0$.
<videoflash>zBvBpVtrjA8</videoflash>
With a complete theoretical model, we must estimate the values of our parameters before we can fully construct a computer simulation of the experiment.
Parameters
Several parameters must be estimated for use in the simulation. With the exception of gravitational acceleration and the number of metronomes, all parameters must be estimated with a varying amount of uncertainty. The platform mass contains perhaps the least uncertainty, and is given (in kilograms) by $M=0.0655+N(0.094-m)$, where we include the mass of the metronome minus the bob in the total. The pendulum bob mass is estimated as $0.022kg$; this is only estimated because an exact measurement would require the destruction of borrowed experimental materials.
The pivot damping coefficient, $b$, is estimated from a measurement of the decay time for an undriven oscillation of the metronome, experimentally determined as $t_{decay}=20 s$; the value used for $b$ is thus $b=2m/t_{decay}=0.0022$. The platform damping coefficient, $B$, has a considerable amount of uncertainty; we expect that for our soda cans rolling on a smooth surface, the damping should be very small, so we somewhat arbitrarily pick $B=0.001$.
As far as the parameters corresponding to the modeling of the escapement mechanism are concerned, $\gamma$ is difficult to estimate, but $c$ can be predicted fairly well. For $c$, this is because it is primarily the magnitude of this kick that determines the amplitude of the pendula after several oscillations; we experimentally observe oscillations in the range of about $45^{\circ}$, so we can adjust the value of $c$ accordingly. For our simulation, we have decided to use $\gamma=0.97$ and $c=0.025$, as was used in Wiesenfeld and Borrero-Echeverry\cite{Borrero}.
The pendulum length $l$, the final remaining parameter, is difficult to estimate because of a simplification in the model, different from the metronome we use in our experiment. The simulation models a pendulum with a point mass, $m$, a distance $l$ from the pivot. The metronome, in reality, has two spatially extended masses located at two different distances from the pivot. An attempt to calculate an equivalent distance resulted in $l=0.025 m$; however, this gives a natural frequency for the simulation that is considerably higher than what is experimentally observed. The simulation was run a second time with a new value of $l=0.1m$ to match the natural frequency of the pendulums in the simulation to that of the experiment.
Simulation
Incorporation of the equations and the parameters listed above into a computer model allows for a simple numerical investigation for the cases of $N=2$ through $N=9$. For each case, we run 100 simulations with randomly selected initial conditions (similar to the ``random" initial conditions of the experiment) of approximately constant total energy. The equations of motion are integrated in the simulation up to $\tau=2000$, and synchronization is determined from two criteria: (1) applying the same test from the experimental determination, but applied to the simulation $\phi_j$ variable, and (2) applying a ``strict sync test" in which all peak $\phi_j$ values must be within one time discretization. Runs which fail to satisfy the criteria are noted.
Results & Conclusion
Results
The time to synchronization for experiment and simulation is shown in the two figures to the right. Since the definition of synchronization is somewhat subjective, two synchronization tests are used for the simulation. The first, drawn in blue, uses the same criteria as for the experiment, applied to the time series of $\phi_j$ vaues. This line should be compared to the experimental result, but since the simulation is not subject to experimental error, this criteria may be too lenient. The second simulation line, drawn in green, uses a ``Strict Sync Test" to determine synchronization; the condition for synchronization in this case is that all peak values of $\phi_j$ must be within one time discretization. These two lines are intended to provide a range of simulation synchronization times depending on the stringency of criteria.
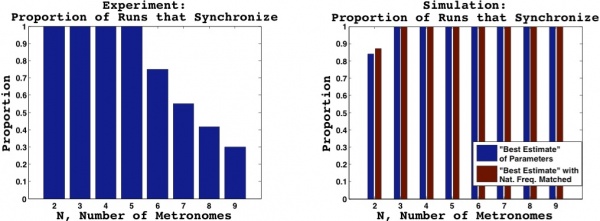
The figure below shows the proportion of runs in both the experiment and simulation that satisfy the synchronization criteria within the allotted time. The decrease in synchronization for $N>5$ in the experiment may be attributable to short data runs, typically of only 2 minutes. Had we waited longer, perhaps synchronization would have been reached; however, more than once we waited as long as the metronome winding would allow, and synchronization was not observed. For the simulation, synchronization is observed in every case except $N=2$. Although this suggests that there are some fundamentally different dynamics between the experiment and simulation, this result in the simulation may be explained as follows. Wiesenfeld and Borrero-Echeverry demonstrated (see Figure 6 of Wiesenfeld and Borrero-Echeverry) that varying the platform damping coefficient can cause the size of the basins of attraction for in phase and antiphase synchronization to expand or contract. We believe that for our particular set of parameters, which differ from those of Wiesenfeld and Borrero-Echeverry, a thin basin of attraction exists for the antiphase state; as we add more mass to the platform, we decrease the value of $\Gamma$ and the antiphase state is no longer an attractor for $N=3$ or higher.
Conclusion
We extend recent theoretical developments in the modeling of coupled oscillators beyond the $N=2$ case. We investigate the time to synchronization for $N$ coupled metronomes both numerically and experimentally, and find considerable agreement between the two, especially when the simulation parameters are altered to match the natural frequency experimentally observed. Discrepancy between simulation and experiment may be attributed to a number of factors, including but not limited to: (1) incorrect estimates of parameters, (2) experimental complexities not captured by the model (e.g. the metronome ``kick" mechanism, a reaction force from the platform, etc.), and (3) limited experimental and numerical statistics.
Future Work
Much work can be done to improve upon this effort. In particular, much work can still be done using the data we have collected. A better algorithm for determining synchronization (in place of our $\epsilon$ method) would likely give more reliable results from this data. Alternative methods include a weighted average to determine the peaks and perhaps a Fourier analysis. Further analysis of our data could extract results such as how frequency changes with $N$ or a quantification of the non-synchronized states that we observed.
In terms of extensions beyond this work, obvious improvements include a better estimate of the simulation parameters and a larger ensemble of data for stronger statistics. Additionally, one could vary any of the parameters and test the agreement between experiment and numerics. The two most appealing parameters to vary are perhaps the natural frequency of the metronomes and the platform mass.
Clearly, there is much to be learned before the phenomenon of synchronization is thoroughly understood, but a solid foundation is being constructed.
References
<references />