Group 6
Nonlinear Dynamical Analysis of Ferrofluid
Ferrofluids exibit nonlinear dynamical behavior in response to both static and oscillating external magnetic fields. An experiment will be developed to isolate a single peak response of ferrofluid to an electromagnetic field generated by a hertzien coil. The apparatus will be configured such that a single peak will be isolated. The response will be observed with a high-speed camera. First a static magnetic field will be applied. This is expected to result in nonlinear surface behavior accompanied by a hysteresis effect. Spontaneous peak formation will be observed at a critical field magnitude. We will examine this response and relate an established qualitative model. A critical magnitude in which spontaneous peak formation is induced (normal field instability), will be observed and analytically correlated to the model. The expected subcritical instability will be observed and the resulting peaks peak characteristics will be analyzed. Next, a thermal component will be introduced and a corresponding term added to the dynamical equation to account for this effect. This nonlinear surface oscillating bifurcation is rarely studied or observed.
Background
The formation of ferrofluid liquid crests due to magnetic induction was first explored in seminal work by Cowley and Rosensweig in 1967 [6]. They provided a theoretical basis for the critical level of magnetization for the onset of the instability at which peaks form and coined this phenomenon the “Rosensweig instability”. They validated the theory with experimentation by providing a uniform magnetic field, via a Helmholtz coil pair, to a small amount of fluid located between the coils. Oddly, the induced peaks were hexagonal in shape, and measurement of the distances between the peaks showed a close comparison to theoretical predictions. Furthermore, their work showed that the instabilities were governed by the stabilizing gravitational force and interfacial tension, which agreed with established knowledge of these systems [7]. Since then, ferrofluids have been shown to have interesting nonlinear behavior in the presence of magnetic fields as drops on a surface [1], fluid pumped under magnetic stress [8, 9], single [2] and multiple [10] peak formation in standing and oscillating magnetic fields, and propagation of these waves under temporally and spatially modulated magnetization [11]. Ferrofluids are ideal for a range of applications, including…. Ferrofluids also provide many ideal characteristics for studying their surface instabilities. One includes the fluid’s colloidal and thermal stability. The magnetic particles remain in suspension, without agglutinating and precipitating out of solution. This is facilitated by thermal energy (Brownian motion) but is largely due to a surfactant coating on each particle that prevents the particles from permanently binding to each other [12]. The thermal stability has also been documented. Over several weeks of maintaining the fluid at temperatures above 150°C in seals jars, ferrofluids show minimal change in viscosity and magnetic permeability at 27°C before and after heating [cite kipp’s thermal paper]. Furthermore, ferrofluids are typically capable of responding to a magnetic field in temperatures ranging from -55°C (outer space) and 200°C.
Experimental Apparatus
Overall Apparatus
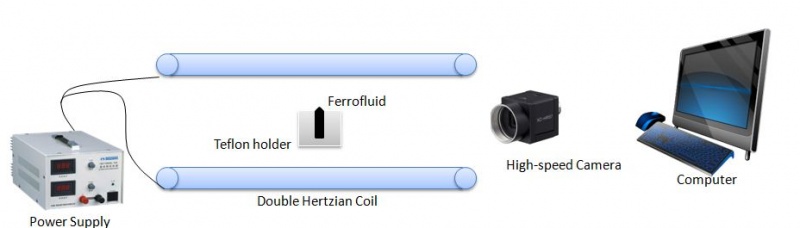
The overall apparatus will consist of the following parts list and configured according to Figure 1. The Teflon fluid holder is used to obtain a flat fluid surface taking advantage of the low surface tension of the material. The Teflon holder will be fabricated by drilling a 3mm diameter and 12mm deep hole into the bulk Teflon and then creating a 30 degree countersink. The ferrofluid is then injected into the hole. The current controlled power supply will drive the magnetic field generated within the herzian coils and the event monitored using a high-speed camera. Computer software will be used to correlate the height of the peak by a pixel/length relationship.
Parts list
- Hertzion Coil
- Teflon Fluid Holder
- Power Supply
- High-speed Camera
- Ferrofluid - EFH-1
Hertzian Coil
They dynamic response of the ferrofluid depends directly on the control parameter, the magnetic field. An understanding of the field magnitude and profile are essential in obtaining consistent and predictable results. The vector potential and field of a circular loop is given in Smythe [1] and elliptic integrals given by ref [2]. The model was expanded to account for two coils by adding an additional term and subtracting out the separation space (d). The model was verified with parameters given in ref [3], by inputting the given coil dimensions and input current. The magnetic field strength of the model (8.179*10^3*A/m) closely matches the stated value of (8 *10^3*A/m) for an assumed coil spacing equal to coil radius. Figure 2 shows a cross sectional view of the coils and the chosen reference origin “O” used to define the system. See Appendix for calculations.
Estimated dimensions of the coil identified for use with this project were entered into the model. Figure 3 shows the magnetic field strength and magnetic induction profile for this proposed system.
Assuming 5 Amp input, a modest magnetic induction of 4 mT is expected at 90deg. The angle and magnitude did not deviate significantly (<3.3%) within a 10cm diameter.
Experimental Procedure
References
[1] W. R. Smythe, Static and Dynamic Electricity, 3rd ed.: A SUMMA Book, 1989.
[2] (October 12). keisan. Available: http://keisan.casio.com/keisan/error.php
[3] T. Mahr and I. Rehberg, "Nonlinear dynamics of a single ferrofluid-peak in an oscillating magnetic field," Physica D, vol. 111, pp. 335-346, Jan 1998.
Potter's references for the background section:
[1] V. Sterr, R. Krauß, K. I. Morozov, I. Rehberg, A. Engel, and R. Richter, New Journal of Physics 10 (2008) 063029.
[2] T. Mahr and I. Rehberg, Physica D 111 (1997) 335.
[3] L. Rudnick, Synthetics, Mineral Oils, and Bio-Based Lubricants: Chemistry and Technology, CRC Press, 2005.
[4] C. Rau, E. Umlauf, and H. Kuffner, NUCLEAR INSTRUMENTS & METHODS IN PHYSICS RESEARCH SECTION B-BEAM INTERACTIONS WITH MATERIALS AND ATOMS 13 (1986) 594. [5] D. Vollath, Nanomaterials: An Introduction to Synthesis, Properties and Applications, Wiley-VCH. [6] M. D. Cowley and Rosenswe.Re, Journal of Fluid Mechanics 30 (1967) 671. [7] J. Melcher, Field-Coupled Surface Waves, MIT Press, 1963. [8] R. Krauß, M. Liu, B. Reimann, R. Richter, and I. Rehberg, New Journal of Physics 8 (2006) 18. [9] R. Krauß, B. Reimann, R. Richter, I. Rehberg, and M. Liu, Applied Physics Letters 86 (2005) 024102. [10] T. Mahr and I. Rehberg, Europhysics Letters 43 (1998) 23. [11] A. Beetz, C. Gollwitzer, R. Richter, and I. Rehberg, Journal of Physics: Condensed Matter 20 (2008) 204109. [12] R. E. Rosensweig, Ferrohydrodynamics, Cambridge University Press, 1993.