Group 4 2014: Difference between revisions
No edit summary |
PatrickChang (talk | contribs) No edit summary |
||
| (33 intermediate revisions by one other user not shown) | |||
| Line 3: | Line 3: | ||
''Group Members: Alex Lind, Cristian Salgueiro, Casey Trimble'' | ''Group Members: Alex Lind, Cristian Salgueiro, Casey Trimble'' | ||
[[Media:jumping-aerated-granular.pdf|Final Report]] | |||
== Introduction == | == Introduction == | ||
[[File:BoxApparatus.JPG | thumb | 150px | The jumping robot apparatus used in the variable spring experiments, courtesy of the Georgia Tech CRAB Lab.]] | [[File:BoxApparatus.JPG | thumb | 150px | The jumping robot apparatus used in the variable spring experiments, courtesy of the Georgia Tech CRAB Lab.]] | ||
Granular media present special challenges and benefits to terrestrial animals. When it is well packed, a granular medium may behave as a solid. When loosely packed, the particles in the medium are allowed to flow when forces are exerted on them. For a jumping animal or robot, this property of a loosely packed substrate reduces the efficiency of a jump. | Granular media present special challenges and benefits to terrestrial animals. When it is well packed, a granular medium may behave as a solid. When loosely packed, the particles in the medium are allowed to flow when forces are exerted on them. For a jumping animal or robot, this property of a loosely packed substrate reduces the efficiency of a jump. | ||
| Line 13: | Line 15: | ||
== Theory and Previous Work== | == Theory and Previous Work== | ||
[[File:Simulation.png | | [[File:Simulation.png | thumb | left | 310px | Theoretical predictions of jump height normalized to forcing amplitude versus the nondimensional parameter, mg/kA]] | ||
===Hard Ground=== | |||
Preliminary research carried out in the CRAB Lab on the dynamics of jumping on hard ground predicted an exponential relationship between nondimensionalized jump height and the nondimensional paramter mg/kA where A is the amplitude of oscillation of the motor acting on the jumper. This relationship can be seen in the figure below | Preliminary research carried out in the CRAB Lab on the dynamics of jumping on hard ground predicted an exponential relationship between nondimensionalized jump height and the nondimensional paramter mg/kA where A is the amplitude of oscillation of the motor acting on the jumper. This relationship can be seen in the figure below | ||
In this case, jump height is nondimensionalized by the amplitude of the motor oscillations. For large values of $\alpha$, the single jump (solid) performs better than the stutter jump (dashed). A transition point occurs at $\alpha \approx 0.1$. Below this value, the stutter jump performs better | In this case, jump height is nondimensionalized by the amplitude of the motor oscillations. For large values of $\alpha$, the single jump (solid) performs better than the stutter jump (dashed). A transition point occurs at $\alpha \approx 0.1$. Below this value, the stutter jump performs better. | ||
The performance of the single and stutter jumps are also very dependent on the frequency of the forcing function. Theoretical predictions and past experiments have determined the optimal frequency of the forcing function for both kinds of jumps. In experiment, we will vary the frequency to further understand the dependence of jump height on input frequency. | |||
===Granular Media=== | |||
The motion of an intruder in granular media can be modeled by: | The motion of an intruder in granular media can be modeled by: | ||
| Line 27: | Line 38: | ||
\end{equation} | \end{equation} | ||
The first term on the right side of \eqref{eq: | The first term on the right side of \eqref{eq:response} acts as a one-way spring as the GM compacts beneath the foot of the intruder, and the second term is comparable to a drag force proportional to the intruder's velocity squared. Additional terms may be added to improve the accuracy of this model; one of the most important terms omitted from the above equation is an additive mass model. The idea is that more of the GM sticks to the foot as it spends more time in the medium, thus adding mass and affecting several of the forces. This term is crucial when studying stutter jumps in GM; however for the scope of this study, such higher order corrections can be ignored. This experiment will look at varying experimental parameters in order to observe the change of the coefficients in the equation of motion. | ||
== Apparatus == | == Apparatus == | ||
[[File:ExptSetup.PNG | thumb | left | 150px | Simple schematic of the jumping robot apparatus.]] | |||
The experiment utilizes an existing jumping robot in the Georgia Tech CRAB Lab. The diagram {DOSOMETHINGHERE} shows a schematic of the apparatus. The robot jumps on GM in a box resting above an air duct. In a simple jump, a linear actuator imposes a downward force on the rod, forcing the robot foot into the GM. The spring contracts, and the actuator is released causing the robot to jump. Both the actuator and the air flow are controlled and systematically varied in LabView. | |||
In addition to varying air flow, we vary the spring constant of the foot. Our trials cover a range of flow rates for four different spring constants. We control the spring constant with a variable length spring, shown below. | |||
Data is collected with a force sensor on the jumper and a high speed camera. The force sensor records the force of the motor on the rod, and the camera tracks the motion of a tracking marker on the rod. With force, position, and time data, we show the change in jump dynamics as air flow and spring constant are varied. We compare our results to the theoretical predictions of the CRAB Lab. | |||
== Methods == | == Methods == | ||
We first summarize the construction of the spring, then define the parameter space of our trials. | We first summarize the construction of the spring, then define the parameter space of our trials. | ||
===Automated Variable Spring=== | |||
[[File:varSpring.jpg | thumb | right | 310px | The variable spring apparatus.]] | |||
| Line 41: | Line 63: | ||
The white screw can be adjusted automatically using a stepper motor, mounted in the black motor case attached to the chassis. The motor is driven by a command in LabView, and turns a shaft that rotates the screw. The top of the motor mount is connected to the jump rod of the robot. | The white screw can be adjusted automatically using a stepper motor, mounted in the black motor case attached to the chassis. The motor is driven by a command in LabView, and turns a shaft that rotates the screw. The top of the motor mount is connected to the jump rod of the robot. | ||
===Experiment Design=== | |||
The parameters varied in the experiments are spring stiffness, jump type, forcing frequency and amplitude, and the substrate parameters. Jumps are made on hard ground, as well as on GM that is continuously fluidized. For fluidized GM trials, the rate of air flow is varied. | The parameters varied in the experiments are spring stiffness, jump type, forcing frequency and amplitude, and the substrate parameters. Jumps are made on hard ground, as well as on GM that is continuously fluidized. For fluidized GM trials, the rate of air flow is varied. | ||
| Line 46: | Line 69: | ||
A series of jumps were performed on hard ground using a constant spring stiffness. | A series of jumps were performed on hard ground using a constant spring stiffness. | ||
For GM trials, four | For GM trials, four values of spring stiffness were chosen. For each stiffness, a series of 128 jumps were performed while alternating between single and stutter jumps and varying both the air flow and frequency of jumps. In total, 2048 jumps were conducted on the granular medium, including mistrials. | ||
In the table below is a summary of the parameters swept through for each experiment. Each number corresponds to the number values assigned to each parameter. "N/A" means that parameter was not varied. | |||
{| border="1" class="wikitable" | |||
|+ Parameter Space | |||
! Parameter | |||
! Hard Ground | |||
! Granular Media | |||
|- | |||
! Jump Type | |||
| style="text-align:center;"|2 | |||
| style="text-align:center;"|2 | |||
|- | |||
! Frequency | |||
| style="text-align:center;"|10 | |||
| style="text-align:center;"|16 | |||
|- | |||
! Spring Constant | |||
| style="text-align:center;"|4 | |||
| style="text-align:center;"|4 | |||
|- | |||
! Amplitude | |||
| style="text-align:center;"|2 | |||
| style="text-align:center;"|N/A | |||
|- | |||
! Media Fluidization | |||
| style="text-align:center;"|N/A | |||
| style="text-align:center;"|4 | |||
|- | |||
|} | |||
==Experiment Videos== | |||
<videoflash>j_CyJBfTNUc</videoflash> | |||
<videoflash>ocFDIMlPMds</videoflash> | |||
==Results== | |||
Using the high speed camera setup, position versus time data was obtained for both the hard ground and GM jumping trials.From this data, the maximum height for each jump was obtained, and a series of plots showing how maximum jump height and the dynamics of the jump varied with the different parameters. | Using the high speed camera setup, position versus time data was obtained for both the hard ground and GM jumping trials.From this data, the maximum height for each jump was obtained, and a series of plots showing how maximum jump height and the dynamics of the jump varied with the different parameters. | ||
===Hard Ground Results=== | |||
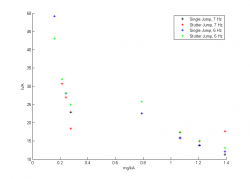
[[File:HardGroundNormOne.png | thumb | left | 250px | Results of hard ground jumps. Plotting max height/A vs. mg/kA]] | |||
[[File:HardGroundEquilTwo.png | thumb | right | 250px | Results of hard ground jumps. Plotting max height/(mg/k) vs. mg/kA]] | |||
To the left and right are the plots for the hard ground jumps. On the left is a plot of the heights normalized to the forcing amplitude versus our nondimensional parameter, $mg/kA$. The plot on the right is similar, except the heights are normalized to the equilibrium position, defined as $mg/k$. | |||
The plot nondimensionalized to forcing amplitude does not match well with theory. In our experimental results, the single jump outperforms the stutter jump at low $\alpha$, but the stutter jump outperforms the stutter jump at high $\alpha$. This is unfortunately contrary to theoretical results. The plot also has a strange decrease in amplitude as $\alpha$ decreases, which is also contrary to theoretical predictions. Part of this discrepancy could be better explained with a finer parameter sweep, specifically testing at more than just two amplitudes. | The plot nondimensionalized to forcing amplitude does not match well with theory. In our experimental results, the single jump outperforms the stutter jump at low $\alpha$, but the stutter jump outperforms the stutter jump at high $\alpha$. This is unfortunately contrary to theoretical results. The plot also has a strange decrease in amplitude as $\alpha$ decreases, which is also contrary to theoretical predictions. Part of this discrepancy could be better explained with a finer parameter sweep, specifically testing at more than just two amplitudes. | ||
The plot nondimensionalized to equilibrium position is a much better match to theory. The frequency parameter was swept over a range of values from $f = 2 ~s^{-1}$ to $f = 12 ~s^{-1}$, but in these results, we only present two of those frequencies for clarity. Compared the the theoretical predictions, the plot is qualitatively similar, but not exact. There is still a discrepancy between optimal performance regions for the single and stutter jump. This may be resolved by a much finer parameter sweep given more time. Specifically, it would be beneficial to probe low-$\alpha$ more finely, as the transition between optimal jump type is supposed to occur around $\alpha = 1$, which our trials hardly reached. | The plot nondimensionalized to equilibrium position is a much better match to theory. The frequency parameter was swept over a range of values from $f = 2 ~s^{-1}$ to $f = 12 ~s^{-1}$, but in these results, we only present two of those frequencies for clarity. Compared the the theoretical predictions, the plot is qualitatively similar, but not exact. There is still a discrepancy between optimal performance regions for the single and stutter jump. This may be resolved by a much finer parameter sweep given more time. Specifically, it would be beneficial to probe low-$\alpha$ more finely, as the transition between optimal jump type is supposed to occur around $\alpha = 0.1$, which our trials hardly reached. | ||
During a number of the hard ground trials, the forcing amplitude was sufficiently high such that the tracking ball left the field of view of the high speed camera. As a result, the position data for those jumps does not contain the true maximum height of the jump. It was therefore necessary to extrapolate the maximum height for those runs. This was done using kinematics based on the time the jumper was in the air and the velocity with which it left the ground. | During a number of the hard ground trials, the forcing amplitude was sufficiently high such that the tracking ball left the field of view of the high speed camera. As a result, the position data for those jumps does not contain the true maximum height of the jump. It was therefore necessary to extrapolate the maximum height for those runs. This was done using kinematics based on the time the jumper was in the air and the velocity with which it left the ground. | ||
Systematically varying the frequency of forcing was found to have a strong effect on the time and amplitude of the maximum height of stiffness and the airflow had smaller effects. | Systematically varying the frequency of forcing was found to have a strong effect on the time and amplitude of the maximum height of stiffness and the airflow had smaller effects. | ||
===Granular Media Results=== | |||
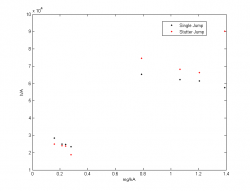
[[File:HeightsPlot.jpg | thumb | 350px | Results for the granular media jumps. Plotting maximum height vs. time]] | |||
In single jumps, the maximum amplitudes were plotted as the frequency of forcing was systematically increased. Shown in Figure , it is evident that there is an optimum jump frequency, which has been found in previous research. The frequency that yielded the highest jump was $5.375Hz$. | In single jumps, the maximum amplitudes were plotted as the frequency of forcing was systematically increased. Shown in Figure , it is evident that there is an optimum jump frequency, which has been found in previous research. The frequency that yielded the highest jump was $5.375Hz$. | ||
| Line 69: | Line 139: | ||
==Conclusions== | ==Conclusions== | ||
The results for the hard ground experiment did not match what was expected from the simulations. The single jump performed better than the stutter jump at lower $\alpha$ values. In order to fully understand the discrepancy between the experiment and simulation, the experiment should be repeated with a finer parameter sweep. | The results for the hard ground experiment did not match what was expected from the simulations. The single jump performed better than the stutter jump at lower $\alpha$ values. In order to fully understand the discrepancy between the experiment and simulation, the experiment should be repeated with a finer parameter sweep. | ||
By exploring the parameter space of a jumper in a granular media, it was shown that the frequency of the jumper has more immediate implications than either the stiffness or the airflow through the medium. It was also shown that there exists a critical frequency for granular media stutter jumps, below which the amplitude of the second maximum is lower than the first maximum; the stutter jump does not perform as expected in this frequency regime. It would be interesting to study this critical frequency further and understand the implications of such a bifurcation. | By exploring the parameter space of a jumper in a granular media, it was shown that the frequency of the jumper has more immediate implications than either the stiffness or the airflow through the medium. It was also shown that there exists a critical frequency for granular media stutter jumps, below which the amplitude of the second maximum is lower than the first maximum; the stutter jump does not perform as expected in this frequency regime. It would be interesting to study this critical frequency further and understand the implications of such a bifurcation. | ||
In broader terms, robots in granular media present an interesting physical problem. For instance, the moon is covered in a layer of granular regolith that can be anywhere from 3 to 20m deep, and a robot operating in such conditions would necessarily have to deal with the effects of granular media. Speculatively, it seems likely that robots would be the ideal tools for further exploration and scientific work on the moon, and further research into the motion of robots in granular media would be useful for future space missions. | In broader terms, robots in granular media present an interesting physical problem. For instance, the moon is covered in a layer of granular regolith that can be anywhere from 3 to 20m deep, and a robot operating in such conditions would necessarily have to deal with the effects of granular media. Speculatively, it seems likely that robots would be the ideal tools for further exploration and scientific work on the moon, and further research into the motion of robots in granular media would be useful for future space missions. | ||
Latest revision as of 10:52, 12 December 2014
Jumping on an Aerated Granular Medium
Group Members: Alex Lind, Cristian Salgueiro, Casey Trimble
Introduction

Granular media present special challenges and benefits to terrestrial animals. When it is well packed, a granular medium may behave as a solid. When loosely packed, the particles in the medium are allowed to flow when forces are exerted on them. For a jumping animal or robot, this property of a loosely packed substrate reduces the efficiency of a jump.
The dynamics of a jumper in a granular medium are complex, and such systems have been studied in both human and robotic cases. In the current study, we expand the parameter space of the previous studies of a simple jumping robot in both granular media and hard ground runs. We also test the extreme case of jumps on an aerated medium, where airflow is introduced from below and allowed to fluidize the medium.
Theory and Previous Work
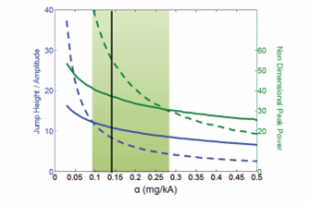
Hard Ground
Preliminary research carried out in the CRAB Lab on the dynamics of jumping on hard ground predicted an exponential relationship between nondimensionalized jump height and the nondimensional paramter mg/kA where A is the amplitude of oscillation of the motor acting on the jumper. This relationship can be seen in the figure below
In this case, jump height is nondimensionalized by the amplitude of the motor oscillations. For large values of $\alpha$, the single jump (solid) performs better than the stutter jump (dashed). A transition point occurs at $\alpha \approx 0.1$. Below this value, the stutter jump performs better.
The performance of the single and stutter jumps are also very dependent on the frequency of the forcing function. Theoretical predictions and past experiments have determined the optimal frequency of the forcing function for both kinds of jumps. In experiment, we will vary the frequency to further understand the dependence of jump height on input frequency.
Granular Media
The motion of an intruder in granular media can be modeled by:
\begin{equation} \label{eq:motion} m_f\ddot{x}_f = F_{spring} + F_{GM} - m_fg \end{equation} and the force from the granular media is most simply modeled with the equation: \begin{equation}\label{eq:response} F_{GM} = k(\text{foot depth}) + \beta(\text{foot speed})^2 \end{equation}
The first term on the right side of \eqref{eq:response} acts as a one-way spring as the GM compacts beneath the foot of the intruder, and the second term is comparable to a drag force proportional to the intruder's velocity squared. Additional terms may be added to improve the accuracy of this model; one of the most important terms omitted from the above equation is an additive mass model. The idea is that more of the GM sticks to the foot as it spends more time in the medium, thus adding mass and affecting several of the forces. This term is crucial when studying stutter jumps in GM; however for the scope of this study, such higher order corrections can be ignored. This experiment will look at varying experimental parameters in order to observe the change of the coefficients in the equation of motion.
Apparatus
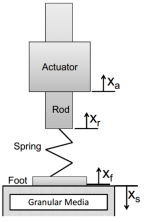
The experiment utilizes an existing jumping robot in the Georgia Tech CRAB Lab. The diagram {DOSOMETHINGHERE} shows a schematic of the apparatus. The robot jumps on GM in a box resting above an air duct. In a simple jump, a linear actuator imposes a downward force on the rod, forcing the robot foot into the GM. The spring contracts, and the actuator is released causing the robot to jump. Both the actuator and the air flow are controlled and systematically varied in LabView.
In addition to varying air flow, we vary the spring constant of the foot. Our trials cover a range of flow rates for four different spring constants. We control the spring constant with a variable length spring, shown below.
Data is collected with a force sensor on the jumper and a high speed camera. The force sensor records the force of the motor on the rod, and the camera tracks the motion of a tracking marker on the rod. With force, position, and time data, we show the change in jump dynamics as air flow and spring constant are varied. We compare our results to the theoretical predictions of the CRAB Lab.
Methods
We first summarize the construction of the spring, then define the parameter space of our trials.
Automated Variable Spring

We expanded on the design of a variable stiffness spring produced by the CRAB Lab using SolidWorks and a MakerBot 3D printer. The green chassis shown in Figure has a threaded interior, along which the white screw in the figure is allowed to turn. The spring is attached to the motor side of the chassis, and terminates in the blue foot. The coils on the motor side of the screw cannot be compressed, and the coils on the foot side of the spring contribute to the compression in a jump.
The white screw can be adjusted automatically using a stepper motor, mounted in the black motor case attached to the chassis. The motor is driven by a command in LabView, and turns a shaft that rotates the screw. The top of the motor mount is connected to the jump rod of the robot.
Experiment Design
The parameters varied in the experiments are spring stiffness, jump type, forcing frequency and amplitude, and the substrate parameters. Jumps are made on hard ground, as well as on GM that is continuously fluidized. For fluidized GM trials, the rate of air flow is varied.
A series of jumps were performed on hard ground using a constant spring stiffness.
For GM trials, four values of spring stiffness were chosen. For each stiffness, a series of 128 jumps were performed while alternating between single and stutter jumps and varying both the air flow and frequency of jumps. In total, 2048 jumps were conducted on the granular medium, including mistrials.
In the table below is a summary of the parameters swept through for each experiment. Each number corresponds to the number values assigned to each parameter. "N/A" means that parameter was not varied.
| Parameter | Hard Ground | Granular Media |
|---|---|---|
| Jump Type | 2 | 2 |
| Frequency | 10 | 16 |
| Spring Constant | 4 | 4 |
| Amplitude | 2 | N/A |
| Media Fluidization | N/A | 4 |
Experiment Videos
<videoflash>j_CyJBfTNUc</videoflash>
<videoflash>ocFDIMlPMds</videoflash>
Results
Using the high speed camera setup, position versus time data was obtained for both the hard ground and GM jumping trials.From this data, the maximum height for each jump was obtained, and a series of plots showing how maximum jump height and the dynamics of the jump varied with the different parameters.
Hard Ground Results
To the left and right are the plots for the hard ground jumps. On the left is a plot of the heights normalized to the forcing amplitude versus our nondimensional parameter, $mg/kA$. The plot on the right is similar, except the heights are normalized to the equilibrium position, defined as $mg/k$.
The plot nondimensionalized to forcing amplitude does not match well with theory. In our experimental results, the single jump outperforms the stutter jump at low $\alpha$, but the stutter jump outperforms the stutter jump at high $\alpha$. This is unfortunately contrary to theoretical results. The plot also has a strange decrease in amplitude as $\alpha$ decreases, which is also contrary to theoretical predictions. Part of this discrepancy could be better explained with a finer parameter sweep, specifically testing at more than just two amplitudes.
The plot nondimensionalized to equilibrium position is a much better match to theory. The frequency parameter was swept over a range of values from $f = 2 ~s^{-1}$ to $f = 12 ~s^{-1}$, but in these results, we only present two of those frequencies for clarity. Compared the the theoretical predictions, the plot is qualitatively similar, but not exact. There is still a discrepancy between optimal performance regions for the single and stutter jump. This may be resolved by a much finer parameter sweep given more time. Specifically, it would be beneficial to probe low-$\alpha$ more finely, as the transition between optimal jump type is supposed to occur around $\alpha = 0.1$, which our trials hardly reached.
During a number of the hard ground trials, the forcing amplitude was sufficiently high such that the tracking ball left the field of view of the high speed camera. As a result, the position data for those jumps does not contain the true maximum height of the jump. It was therefore necessary to extrapolate the maximum height for those runs. This was done using kinematics based on the time the jumper was in the air and the velocity with which it left the ground. Systematically varying the frequency of forcing was found to have a strong effect on the time and amplitude of the maximum height of stiffness and the airflow had smaller effects.
Granular Media Results
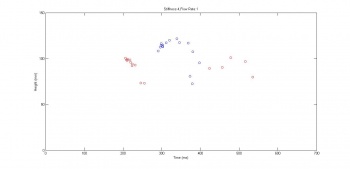
In single jumps, the maximum amplitudes were plotted as the frequency of forcing was systematically increased. Shown in Figure , it is evident that there is an optimum jump frequency, which has been found in previous research. The frequency that yielded the highest jump was $5.375Hz$.
In stutter jumps, there is a range of frequencies at which the second jump in the sequence is higher than the preliminary stutter. Interestingly, the optimum frequency for a single jump is within this range of frequencies, which was from $2.25Hz$ to $3.75Hz$.
Varying the spring stiffness and the airflow in the medium had little effect on the value for the optimal frequency range.
Conclusions
The results for the hard ground experiment did not match what was expected from the simulations. The single jump performed better than the stutter jump at lower $\alpha$ values. In order to fully understand the discrepancy between the experiment and simulation, the experiment should be repeated with a finer parameter sweep.
By exploring the parameter space of a jumper in a granular media, it was shown that the frequency of the jumper has more immediate implications than either the stiffness or the airflow through the medium. It was also shown that there exists a critical frequency for granular media stutter jumps, below which the amplitude of the second maximum is lower than the first maximum; the stutter jump does not perform as expected in this frequency regime. It would be interesting to study this critical frequency further and understand the implications of such a bifurcation.
In broader terms, robots in granular media present an interesting physical problem. For instance, the moon is covered in a layer of granular regolith that can be anywhere from 3 to 20m deep, and a robot operating in such conditions would necessarily have to deal with the effects of granular media. Speculatively, it seems likely that robots would be the ideal tools for further exploration and scientific work on the moon, and further research into the motion of robots in granular media would be useful for future space missions.