Double pendulum: Difference between revisions
No edit summary |
No edit summary |
||
| Line 4: | Line 4: | ||
The double pendulum is a pendulum with another attached at an end. It is a classic example of systems that produce nonlinear dynamics and chaos. | The double pendulum is a pendulum with another attached at an end. It is a classic example of systems that produce nonlinear dynamics and chaos. | ||
== Setup == | |||
[[File:DOUBLEPEND2010.JPG | center | 400px]] | [[File:DOUBLEPEND2010.JPG | center | 400px]] | ||
| Line 9: | Line 11: | ||
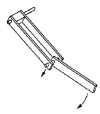
For our experiment, we used a double pendulum consisting of a rod supported by two others. The pendulum was connected to supports that could sinusoidally oscillate in the vertical direction at relatively low frequencies. Simulation was done via MATLAB | For our experiment, we used a double pendulum consisting of a rod supported by two others. The pendulum was connected to supports that could sinusoidally oscillate in the vertical direction at relatively low frequencies. Simulation was done via MATLAB | ||
== Experiment == | |||
We observed the motion of the pendulum at various initial positions, and noted whether it flips or not. If it did, the time it took was measured. | We observed the motion of the pendulum at various initial positions, and noted whether it flips or not. If it did, the time it took was measured. | ||
| Line 18: | Line 22: | ||
(see video below). The same method was used for the forced case. | (see video below). The same method was used for the forced case. | ||
== Simulation == | |||
Using MATLAB, we simulated the motion of the pendulum at various initial conditions. The theory we mainly referenced can be found here | Using MATLAB, we simulated the motion of the pendulum at various initial conditions. The theory we mainly referenced can be found here | ||
The green dots represent cases that, from our experiment, did flip. The red dots represent cases that did not. Note the good agreement of theory and experiment. | The green dots represent cases that, from our experiment, did flip. The red dots represent cases that did not. Note the good agreement of theory and experiment. | ||
Revision as of 09:31, 12 January 2012
Double pendulum
Group members:
The double pendulum is a pendulum with another attached at an end. It is a classic example of systems that produce nonlinear dynamics and chaos.
Setup

From left: Sang-Hyun Rah, Michael Clark, John Robinson, Jacob Blumoff
For our experiment, we used a double pendulum consisting of a rod supported by two others. The pendulum was connected to supports that could sinusoidally oscillate in the vertical direction at relatively low frequencies. Simulation was done via MATLAB
Experiment
We observed the motion of the pendulum at various initial positions, and noted whether it flips or not. If it did, the time it took was measured.
This was done by recording the motion of the pendulum with a high speed camera, and using a program that tracked the motion of the lower bar of the pendulum.
(see video below). The same method was used for the forced case.
Simulation
Using MATLAB, we simulated the motion of the pendulum at various initial conditions. The theory we mainly referenced can be found here
The green dots represent cases that, from our experiment, did flip. The red dots represent cases that did not. Note the good agreement of theory and experiment.