Group 6: Difference between revisions
No edit summary |
|||
| Line 23: | Line 23: | ||
They dynamic response of the ferrofluid depends directly on the control parameter, the magnetic field. An understanding of the field magnitude and profile are essential in obtaining consistent and predictable results. The vector potential and field of a circular loop is given in Smythe [1] and elliptic integrals given by ref [2]. The model was expanded to account for two coils by adding an additional term and subtracting out the separation space (d). The model was verified with parameters given in ref [3], by inputting the given coil dimensions and input current. The magnetic field strength of the model (8.179*10^3*A/m) closely matches the stated value of (8 *10^3*A/m) for an assumed coil spacing equal to coil radius. Figure 2 shows a cross sectional view of the coils and the chosen reference origin “O” used to define the system. See Appendix for calculations. | They dynamic response of the ferrofluid depends directly on the control parameter, the magnetic field. An understanding of the field magnitude and profile are essential in obtaining consistent and predictable results. The vector potential and field of a circular loop is given in Smythe [1] and elliptic integrals given by ref [2]. The model was expanded to account for two coils by adding an additional term and subtracting out the separation space (d). The model was verified with parameters given in ref [3], by inputting the given coil dimensions and input current. The magnetic field strength of the model (8.179*10^3*A/m) closely matches the stated value of (8 *10^3*A/m) for an assumed coil spacing equal to coil radius. Figure 2 shows a cross sectional view of the coils and the chosen reference origin “O” used to define the system. See Appendix for calculations. | ||
| Line 29: | Line 28: | ||
Assuming 5 Amp input, a modest magnetic induction of 4 mT is expected at 90deg. The angle and magnitude did not deviate significantly (<3.3%) within a 10cm diameter. | Assuming 5 Amp input, a modest magnetic induction of 4 mT is expected at 90deg. The angle and magnitude did not deviate significantly (<3.3%) within a 10cm diameter. | ||
==Experimental Procedure== | ==Experimental Procedure== | ||
Revision as of 20:16, 12 October 2011
Nonlinear Dynamical Analysis of Ferrofluid
Ferrofluids exibit nonlinear dynamical behavior in response to both static and oscillating external magnetic fields. An experiment will be developed to isolate a single peak response of ferrofluid to an electromagnetic field generated by a hertzien coil. The apparatus will be configured such that a single peak will be isolated. The response will be observed with a high-speed camera. First a static magnetic field will be applied. This is expected to result in nonlinear surface behavior accompanied by a hysteresis effect. Spontaneous peak formation will be observed at a critical field magnitude. We will examine this response and relate an established qualitative model. A critical magnitude in which spontaneous peak formation is induced (normal field instability), will be observed and analytically correlated to the model. The expected subcritical instability will be observed and the resulting peaks peak characteristics will be analyzed. Next, a thermal component will be introduced and a corresponding term added to the dynamical equation to account for this effect. This nonlinear surface oscillating bifurcation is rarely studied or observed.
Background
Literature Review
Hertzian Coil
Ferrofluid
Experimental Apparatus
Overall Apparatus
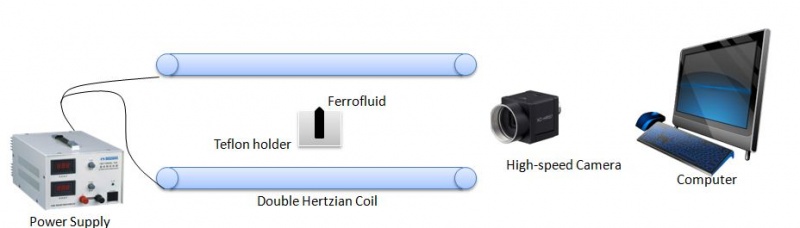
The overall apparatus will consist of the following parts list and configured according to Figure 1. The Teflon fluid holder is used to obtain a flat fluid surface taking advantage of the low surface tension of the material. The Teflon holder will be fabricated by drilling a 3mm diameter and 12mm deep hole into the bulk Teflon and then creating a 30 degree countersink. The ferrofluid is then injected into the hole. The current controlled power supply will drive the magnetic field generated within the herzian coils and the event monitored using a high-speed camera. Computer software will be used to correlate the height of the peak by a pixel/length relationship.
Parts list
- Hertzion Coil
- Teflon Fluid Holder
- Power Supply
- High-speed Camera
- Ferrofluid - EFH-1
Hertzian Coil
They dynamic response of the ferrofluid depends directly on the control parameter, the magnetic field. An understanding of the field magnitude and profile are essential in obtaining consistent and predictable results. The vector potential and field of a circular loop is given in Smythe [1] and elliptic integrals given by ref [2]. The model was expanded to account for two coils by adding an additional term and subtracting out the separation space (d). The model was verified with parameters given in ref [3], by inputting the given coil dimensions and input current. The magnetic field strength of the model (8.179*10^3*A/m) closely matches the stated value of (8 *10^3*A/m) for an assumed coil spacing equal to coil radius. Figure 2 shows a cross sectional view of the coils and the chosen reference origin “O” used to define the system. See Appendix for calculations.
Estimated dimensions of the coil identified for use with this project were entered into the model. Figure 3 shows the magnetic field strength and magnetic induction profile for this proposed system.
Assuming 5 Amp input, a modest magnetic induction of 4 mT is expected at 90deg. The angle and magnitude did not deviate significantly (<3.3%) within a 10cm diameter.
Experimental Procedure
References
[1] W. R. Smythe, Static and Dynamic Electricity, 3rd ed.: A SUMMA Book, 1989.
[2] (October 12). keisan. Available: http://keisan.casio.com/keisan/error.php
[3] T. Mahr and I. Rehberg, "Nonlinear dynamics of a single ferrofluid-peak in an oscillating magnetic field," Physica D, vol. 111, pp. 335-346, Jan 1998.