Group 3 2012

Chaos Circuits

Patrick Chang, Edward Coyle, John Parker, Majid Sodagar

The nonlinear dynamics of Chua’s circuit and its applications to communications is studied. Chaos is realized, and is investigated by calculating the Lyapunov exponent for the system. A three dimensional phase portrait for the characteristic “double scroll” is reconstructed from the two dimensional image, from which the correlation dimension is calculated. This experiment was done by designing Chua’s circuit in the laboratory and comparing results to a simulation.

Introduction

Figure 1: Two Chua Circuits on a single breadboard

Chaos is aperiodic long-term behavior in a deterministic system that exhibits sensitive dependence on initial conditions [Strogatz2001]. There are many applications for chaotic systems, such as predicting nonlinear flow in the atmosphere, understanding the dynamics in cardiac arrhythmias, and handwritten character recognition. Certain studies show that a chaotic system made of circuits can produce novel musical sounds [Chua 1994]. However, in this experiment, we focus more on the applications of a chaotic system in communication. Chaotic signals are usually broad-band, noise like, and difficult to predict [Cuomo1993]. Therefore, chaotic systems are suitable for carrying information. In digital communication, sinusoidal carriers are used because they have optimal bandwidth efficiency and it is easier to reconstruct the original signal. However, their high power spectral density causes a high level of interference and enhances the probability of interception by other receivers [Arena2006]. Chaotic carriers can solve this problem. A chaotic transmitter can send the desired information masked by chaotic signals. This masked signal is then transmitted to the destination, and the signal might be intercepted on the way, but would not be decoded without the masking chaotic signal. At the destination, another chaotic signal generator will be synchronized with the chaotic signal generator at the transmitter and thus produce the exact replica of the masking chaotic signal. The masked signal will then be demodulated by subtracting the masking signal from it to reveal the desired information hidden within [Dedieu1993]. Also, broadband information carriers enhance the robustness of communication and are less vulnerable to interference from narrow-band disturbance. This is the basis of spread-spectrum communication techniques, such as the code division multiple access (CDMA) protocol used in the Global Positioning System (GPS) and in the third generation of mobile telephones [Argyris2005].

In order to achieve masking information in chaotic signals to obtain secure communication, the chaotic oscillators, transmitter and receiver, must be synchronized. Initially, we wanted to achieve synchronization between two or more Chua's circuits acoustically [Harada1996] for the following reasons. Chua's circuit, introduced to the world by Leon Chua in 1983[Wikipedia], is the simplest autonomous circuit that can exhibit a bifurcation and generate chaos, because it satisfies the three criteria for displaying chaotic behavior: containing one or more nonlinear components, one or more locally active resistor, and three or more energy-storage devices [Wikipedia]. It has been a very suitable subject for studying dynamical chaos by means of both laboratory experiments and computer simulations [Harada1996]. Acoustic coupling enables us to adjust various parameters to achieve synchronization, e.g. wave amplitude, feedback time delay, characteristic of media between the oscillators, etc.

However, after setting up our circuits and the acoustic component, we found out that the parts we had are too weak to communicate with the other circuit. Instead, in the process of building up the Chua’s circuits and adjusting their parameters to find chaotic signal, we found some interesting nonlinear behavior of the Chua’s circuit. So we decided to focus on characterizing the nonlinear dynamics of the Chua’s circuit. People have been characterizing Chua’s circuits by computer simulation, so we want to do it from an experimental point of view.

Design and Parts

Chua's Circuit

Figure 1: Circuit diagram of Chua's Circuit used for this experiment

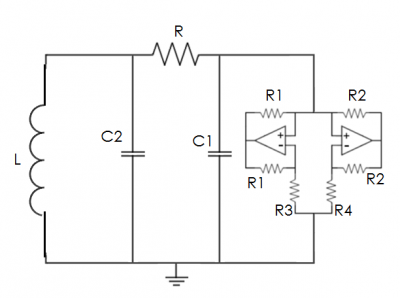
Figure 1 shows a typical Chua circuit. There are three main components to the circuit: the pair of capacitors, the inductor, and Chua's diode. Chua's diode is considered everything to the right of the C1 capacitor in Figure 1, and it is this part that causes the circuit to be nonlinear. Without this component, the circuit is a type of RLC circuit that will exhibit periodic behavior. The op-amp is used to drive the two diodes with a varying voltage. As the voltage varies, one of the diodes may cut off current going both ways if the voltage drops below the diode's cut-in voltage. This on/off behavior of the diodes drastically changes the circuit and causes chaotic behavior.

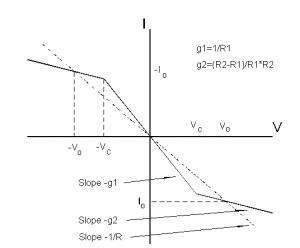
Chua’s circuit can be built several different ways. This experiment replicated the circuit diagram in Figure (1). It has four major components: (1) a variable resistor, whose resistance acts as the control variable, (2) two capacitors, whose electrical responses act as the dependent variables, (3) an inductor, and (4) Chua’s diode, which is the source of the nonlinearity in the system. The electrical response of Chua’s diode is shown in Figure (2) and corresponds to the function g(V) in the differential equations.

Figure (2) shows a picture of the circuit. Here there are actually two Chua circuits on one circuit board, but all of the experiments were carried out using only one. The project to study how two Chua circuits coupled together, either electrically or acoustically, was abandoned to study the dynamics of a single Chua circuit. As it turns out, the dynamics of a single Chua circuit are complex enough to merit further study.

Chua’s circuit was hooked up to an oscilloscope and external computer that sampled the voltages across the two capacitors at 48,000 samples per second. Data was collected for several different values of the variable resistance.

Parts

Figure 2: IV curve for Chua's Diode

• 3 - 10 nF Capacitors
• 3 – 100 nF Capacitors
• 3 – 15 mH Inductors
• 3 – Variable Resistors in kΩ range
• 6 – 220 Ω Resistors
• 6 – 22 kΩ Resistors
• 3 – 2.2 kΩ Resistors
• 3 – 3.3 kΩ Resistors
• 6 – MA23L3 Ultrasonic Transducers (not used)
• 3 – TL082

The Equations

<math>\frac {dx}{dt} = α[y - x - g(x)]</math>

<math>\frac {dy}{dt} = x - y + z</math>

<math>\frac {dz}{dt} = -βy</math>

x(t) is the voltage across C1, y(t) is the voltage across C2, and z(t) is the current across L. α and β depend on the values of the various circuit components. The function g(x) is the source of the non-linearity, and it depends on the specifications of Chua's diode. The IV curve of a Chua's Diode is shown in Figure 2, and this is the piece-wise g(x) function used in the equations. For simulations of these equations, see references [1] and [4].

Procedure

The first step in this experiment is to create a working Chua's circuit that exhibits chaotic behavior. This is measured using an oscilloscope. Chaos is achieved when the phase plane takes on a double scroll attractor, as shown in Figure 3. This can be achieved by varying the resistance of the resistor R in Figure 1. Once a Chua's circuit is successfully built, the circuit needs to be modified with an ultrasonic transducer so that the circuit produces acoustic output. Once again, chaos has to be achieved as measured by an oscilloscope. Once this is done, a duplicate will be made so that the two can become acoustically coupled. Measurements of the voltages inside both coupled circuits will be compared to see if there is any sort of synchronization.

Experimental Results

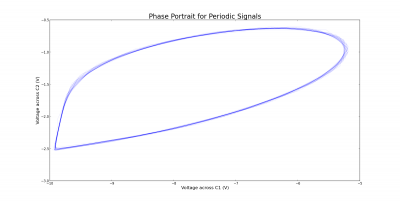
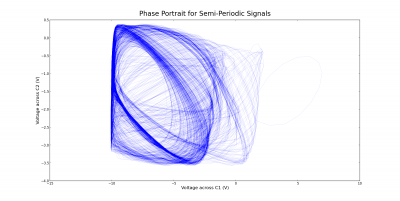
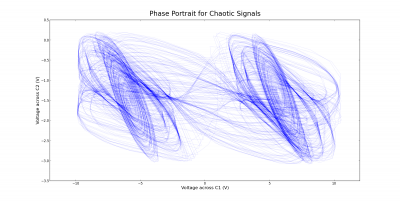
There are several different routes to chaos in Chua’s circuit. In the experiment, the route observed was periodic behavior, followed by a “screw attractor”, and finally chaotic behavior, referred to as a “double scroll” in Chua’s circuit (Ref. Harada 1996). This contrasts to period doubling, whose requirements of the function g(V) did not meet the specifications of our circuit (Chua 1993). The meaning of a “screw attractor” is most evident by looking at the phase space diagram for the two voltages in figure (4). Out of the periodic behavior, a single chaotic attractor was born as the resistance increased. This may be referred to as “semi-periodic” behavior, meaning that it is almost periodic, but has some chaotic aspects.

When the resistance was increased further, another attractor was born, forming a double scroll. The phase portrait for this behavior is shown in Figure (5). Trajectories in phase space are confined to this double scroll and orbit around these two attractors in a complicated way. It is this complicated behavior that we wish to analyze.

Figure 1: Phase space diagram for periodic behavior

Figure 1: Phase space diagram for semi-periodic behavior

Figure 1: Phase space diagram for chaotic behavior

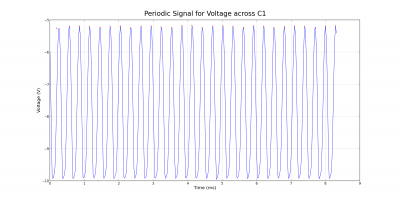
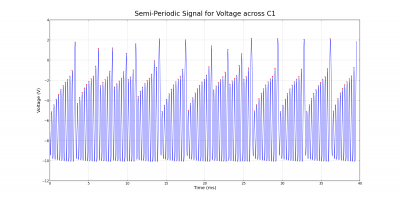
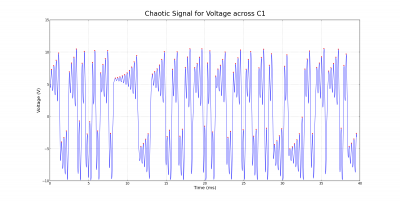
The periodic and chaotic behavior can also be observed by looking at voltage-time plots instead of phase space diagrams. The corresponding cases for the voltage across the capacitor C1 are shown below. Notice the differences between the semi-periodic and chaotic plots. Although the semi-periodic plot appears to be somewhat chaotic and irregular, it is not as definite as the chaotic plot.

Figure 1: Periodic signal across a capacitor

Figure 1: Semi-periodic signal across a capacitor

Figure 1: Chaotic signal across a capacitor

Lyapunov Exponent

The Lyapunov exponent is a measure of how two nearby trajectories diverge over time.

<math>|δ Z(t)| = e^λ ^t |Z(0)|</math>

If the value is positive, then any two nearby trajectories diverge exponentially, and chaos results. If the value is negative, then two trajectories converge exponentially and chaos is not observed. Knowing the Lyapunov exponent for a system is a good measure of how chaotic the system is.

Two nearby points were chosen in phase space by scanning the data and finding any two points that were separated by no more than 0.0075 V across each capacitor. These two points were of course separated in time by quite a bit. Finding points any closer would prove difficult or impossible despite having data collected over about ten seconds (an incredible amount of time for the dynamics of the circuit, which can change rapidly on the order of a millisecond). Two nearby trajectories in phase space are shown in figure (6) over a short time. In such a time, these trajectories are nearly locked on and only separate by a small amount in the end. Figure (7) shows the two trajectories over a long time. By this time, the trajectories have completely different behavior and no longer resemble each other. The system is chaotic, for a small separation in initial conditions has grown to something enormous. Figure (8) emphasizes the divergence by showing how the two trajectories compare on the voltage-time plot. They begin locked on, but after a few milliseconds they take on completely different behavior.

A true description of two nearby trajectories requires n Lyapunov exponents in n-dimensional space. Each independent variable contributes to the total chaos of the system. This was not the method used here. Instead, the maximal Lyapunov exponent was measured. The maximal Lyapunov exponent is a measure of how the distance between two nearby trajectories in phase space diverges in time (ref = strogatz).

Only a single value for the Lyapunov exponent is obtained using this method. However, the Lyapunov exponent depends on the initial conditions (ref = strogatz) and therefore depends on which attractor the trajectories start in, since the two attractors are not identical. So two Lyapunov exponents are expected, one for each attractor. In determining the Lyapunov exponent for each attractor, it was important to ensure that these trajectories did not leave the attractor they started in too quickly. Otherwise, the calculated value would be influenced by both attractors. Keeping in mind that the Lyapunov exponent varies in phase space, an average Lyapunov exponent can be defined for the whole system.

The Lyapunov exponent is determined by plotting the log of the distance between the two trajectories as a function of time. As a result, linear behavior is expected. One of these plots is shown in Figure (9) and a line is fitted to the first part. There is a saturation point where the linear behavior disappears because the trajectories are confined to the attractor.

This procedure was done for a number of initial conditions (each of which do not leave the attractor they start in too quickly) and an average was calculated for each attractor. The left attractor and right attractor have an average Lyapunov exponent of 1.0 and 1.7, respectively. These averages have a standard deviation of around 0.3, although the dependence of the Lyapunov exponent on position in phase space implies the distribution isn’t normal anyways; there is some natural variance in the system. The variance obtained is due to this, but also due to the inexact measurement of the Lyapunov exponent, for there is no exact method for fitting a line to the curve. In addition, a t_horizon was defined from the average Lyapunov exponent of the system, 1.33.

Insert Equation (pg 322, strogatz)

Here, a is the tolerance level, chosen to be 0.1 V, and (delta) is the uncertainty in measurement, chosen to be 0.001 V. The t_horizon comes out to 3.46 ms. So after this time, the uncertainty has grown to 0.1 V. This is only a rough model.

A note: nearby trajectories were obtained by tracing though the data and finding two points in phase space (which were separated in time by a large amount) that were close. I only accepted points that were within 0.0075 V across C1 and C2. So the initial separation was no larger than 0.0075 * (sqrt(2)) in phase space. The trajectories for each initial condition were then obtained by looking at the data following these two points.

A note: finding literature to compare this to is difficult since there is no direct way of calculating the Lyapunov exponent and since it will likely depend on the parameters in the differential equation (a simulation would be a better comparison)

References

Websites

[1] http://crossgroup.caltech.edu/chaos_new/Chua.html

[2] http://www.wellgainelectronics.com/muratama23l3.aspx

[3] http://www.chuacircuits.com/

[4] http://www.chuacircuits.com/sim.php

[5] http://nonlinear.eecs.berkeley.edu/chaos/chaos.html

Literature

[6] S. H. Strogatz, Nonlinear Dynamics and Chaos: With Applications To Physics, Biology, Chemistry, And Engineering (Studies in Nonlinearity). Westview Press, 2001, p. 512.

[7] K. Cuomo, “Synchronization of Lorenz-based chaotic circuits with applications to communications,” Circuits and systems II: …, vol. 40, no. 10, pp. 626–633, 1993.

[8] P. Arena, A. Buscarino, L. Fortuna, and M. Frasca, “Separation and synchronization of piecewise linear chaotic systems,” Physical Review E, vol. 74, no. 2, pp. 1–11, Aug. 2006.

[9] A. Argyris, D. Syvridis, L. Larger, V. Annovazzi-Lodi, P. Colet, I. Fischer, J. García-Ojalvo, C. R. Mirasso, L. Pesquera, and K. A. Shore, “Chaos-based communications at high bit rates using commercial fibre-optic links.,” Nature, vol. 438, no. 7066, pp. 343–6, Nov. 2005.

[10] Y. Harada, K. Masuda, and A. Ogawa, “Dynamical behavior of acoustically coupled chaos oscillators,” Fractals-an Interdisciplinary …, 1996.