Group 5 2014

Members: Caligan, Lucas, Li, Norris

Introduction

In 1665, the Dutch scientist Christiaan Huygens discovered that two pendulum clocks mounted on the same wall synchronize with one another---the bobs swing with the same frequency but exactly out of phase, Huygen. The origin of this effect is weak coupling of the clocks mediated through the wall’s vibrations. Since then, the seemingly old topic of synchronization has developed into one of the most actively studied phenomena, in such diverse contexts as coupled lasers in optics, firing neurons in the brain, synchronous flashing by fireflies and rhythm of applause at concerts. It has been of conceptual interest to scientists in the fields of applied mathematics, nonlinear dynamics, statistical physics and material science.

Outline

The phenomena of synchronization in pendula lying along the same plane has been studied extensively in general. It was shown that several modes can occur in general. The possible configurations are complete synchronization of the system, synchronization of clusters of three or five pendula, or total antiphase synchronization. The paper Perlikowski claims that these phenomena can be observed in the laboratory. An extension of this would be to allow spherical pendula to synchronize along a plane instead of requiring the pendula to be along a straight line of the plane they lie on. This will allow higher dimensionality in the phase space and phenomena that may be observed. A further extension will be to allow the motion of the plane to be controlled by placing it on top of Meissner bodies. This will add more complexity to the system and hopefully more interesting dynamics as well.

Theory

It is easy to write down the system of differential equations for n simple harmonic oscillators coupled together. This takes the form \begin{equation} \dot{\theta}_k(t) = \omega + \frac{k}{n} \sum_{i=1}^n \sin\left(\theta_i(t) - \theta_k(t)\right). \end{equation}

Figure 1: Phases of 11 Coupled Harmonic Oscillators

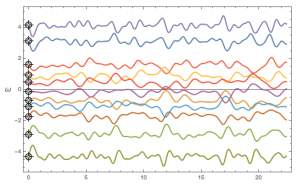
Synchronization phenomena of 11 coupled harmonic oscillators may be seen in Figure 1. The differential equations for a single spherical pendulum are \begin{equation} \begin{aligned} m r^2 \ddot{\theta} - m r^2 \sin\theta \cos\theta \dot{\phi}^2 + m g r \sin\theta &= 0,\\ 2 m r^2 \dot{\theta} \sin\theta \cos\theta \dot{\phi} + m r^2 \sin^2\theta \ddot{\phi} &= 0. \end{aligned} \end{equation} when the length of the pendulum is at a constant radius from its origin.

Methods

The experiment will be conducted with several spherical pendula sitting on a plane. The plane will start out being rested on top of several spheres so that the only contribution to the dynamics of the system is from the pendula themselves. Once this portion of the experiment has been conducted and the result of Perlikowski have been observed, we will move to placing Meissner bodies under the plane. This will allow for an additional nonlinear effects to the dynamics of the system. The team will attempt to produce some of the synchronization phenomena found by theoretical means and possibly other phenomena that were not discovered theoretically.

Before studying the synchronization of coupled pendulum on same base plane, we will first study non-linear dynamics of one pendulum (\autoref{fig:Single2}). A electromagnetic pendulum will be positioned at the center of a base plane, with several Meissner's bodies located randomly underneath the base plane. Experimental parameters such as Meissner's bodies (e.g., the numbers and position of Meissner's bodies), the mass of base plane, the height and weight of pendulum and the magnetic strength of electromagnetic pendulum will all influence the non-linear dynamic behavior of pendulum, those parameters will be evaluated individually.

File:Example.jpg