Group 1: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 9: | Line 9: | ||
This experiment is designed to reproduce the results of quantifying the observance of these waves by Binks and W. van de Water [3]. The expected results should also agree with Zhang and Vinals' [2] prediction of the amplitudes of the standing waves. The experiment will go a step further and not only test the theory out for different fluids (including a non-newtonian fluid), but for different oscillatory patterns (square, sinusoidal,and triangle) . | This experiment is designed to reproduce the results of quantifying the observance of these waves by Binks and W. van de Water [3]. The expected results should also agree with Zhang and Vinals' [2] prediction of the amplitudes of the standing waves. The experiment will go a step further and not only test the theory out for different fluids (including a non-newtonian fluid), but for different oscillatory patterns (square, sinusoidal,and triangle) . | ||
[[File:FaradayExperiment.jpg|right| | [[File:FaradayExperiment.jpg|right| 400 px|]] | ||
# Reproduce the experiments of Binks and Van de Water | # Reproduce the experiments of Binks and Van de Water | ||
Revision as of 18:13, 19 October 2011
Faraday Waves and Nonlinear Patterns
Background
- Eponymously discovered by Faraday[1], Faraday Waves are standing waves on a fluid caused by vertical oscillatory motion. At given frequencies, these standing waves (vibrating at held the driving frequency) give surface paterns of n dimensional rotational symmetry; mainly square, hexagonal, and 8-fold quasi-static patterns. The wavelength of the standing waves are a function of viscosity, surface tension and density. Hence, understanding the relationship between these variables and the wavelength, will allow oscillation frequencies to be selected that produce standing waves of order n.
Previous Experiments
Experiment
This experiment is designed to reproduce the results of quantifying the observance of these waves by Binks and W. van de Water [3]. The expected results should also agree with Zhang and Vinals' [2] prediction of the amplitudes of the standing waves. The experiment will go a step further and not only test the theory out for different fluids (including a non-newtonian fluid), but for different oscillatory patterns (square, sinusoidal,and triangle) .
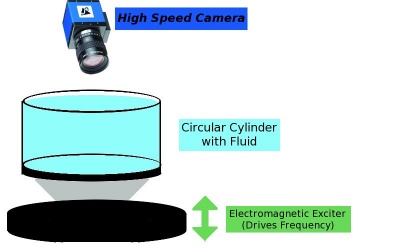
- Reproduce the experiments of Binks and Van de Water
- Fill a 440 mm diameter circular container with 20 mm height of experimental fluid
- Attach a 2 cm thick plate on the bottom of the container and a hollow conical structure attached to an electromagnetic exciter below that.
- Place piezo-electric accelerometers on the cone (one on bottom, two on top) to measure the acceleration cone. This allows control of the oscillation frequency.
- A high speed CCD camera is placed above the container to take snapshots of the standing waves. It is required that the frames per second of the snapshots are greater than the oscillation period of the standing waves.
- The amplitude of the oscillations are controlled by the electromagnetic exciter and increased in small steps (about 1%) where each wave is held for 2000 seconds first before taking 1000 s of images of the waves.
- Measurements of the amplitude of the waves are taken by a laser
- Compare the amplitudes and patterns with theory as a function of driving frequency
- Repeat experiment with another fluid, and a non newtonian fluid and checking if theory is consistent across different fluids.
- Observe the effects of changing the wave form on the standing waves
- Sinusoidal Waves
- Square Waves
- Triangle Waves
Videos of Faraday Waves
Faraday Waves on Cornflour
Faraday Waves set to music
Group Members
- Juan Orphee
- Paul Cardenas-Lizana
- Michael Lane
- Elan Grossman
Sources
- [1] M. Faraday, Philos. Trans. R. Soc. London 121, 319 (1831)
- [2] W. Zhang and J. Viñals, Phys. Rev. E 53, R4286 (1996)
- [3] D. Binks and W. van de Water, Phy. Rev. Lett. 78, 4043 (1997)
- [4] Peilong Chen and J. Vinals, Phys. Rev. Lett, 79, 2670 (1997)
- [5] J. Bechhoefer and B. Johnson, Am. J. Phys, 64, 12 (1996).