Group 2

Plinko game on The Price is Right

Background

Inspired by the game Plinko featured on the popular American television gameshow The Price is Right, the original concept was to investigate potentially chaotic structure within the Plinko system. As will be discussed briefly below, this proved to be more difficult than was initially expected, and the collision based peg system was replaced with a series of magnets to create a magnetic Plinko board.

Problems with Original Plinko

Traditional studies of Plinko and other pinball billiard games have analyzed the aggregate statistics of the outcomes based on the starting position [1,2]. These analyses assume that each puck-pin interaction can only result in one of two possible outcomes: left or right. These analyses also assume that the puck must always continue downward without the possibility for upward motion, and they do not analyze the trajectory or starting conditions in detail.

In order to study this system, a simulation of the system has been created in two ways: using a Runge-Kutta integration method with an event detection loop to detect collisions between the puck and the pegs to solve the puck's motion due to gravity; and a simulation that calculated parabolic trajectories between pegs and root solved for the collisions. For both methods, upon the detection of a collision, the model calculates the reflection angle of the puck about the peg normal at the collision point with a user-defined coefficient of restitution. From this angle, a new initial velocity is determined and the process is iterated from that point. This procedure continues until the puck crossed the lowest row of pegs on the Plinko board.

Exponential divergence of collisions

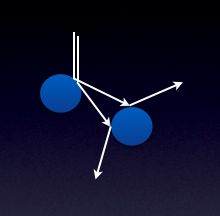
Both methods have significant problems appropriately detecting collisions. The Runge-Kutta integrator often sets the time step so high as to miss collisions due to the simple nature of the equations of motion. Fixing the time step to some small value causes collisions to be detected correctly, but this results in a longer run time as well as the build up of numerical errors in the trajectory. Running two different maximum time steps for the same initial condition results in significantly different trajectories. The parabolic simulation is mostly immune to overstepping collisions at high (>0.8) coefficients of restitution, but for values of the variable low enough to provide the dissipation necessary for the onset of chaos, even the parabolic simulation has singularity issues that led to trajectories clipping the pegs.

In addition to simulation issues, a map of the initial position and velocity against the final cross-slope position reveals that there is no structure in the input space, and there are no basins of attraction within the system to the resolution to which we ran the simulation. Furthermore, no analysis of the data is able to produce a strange attractor. It is determined that this problem did not produce chaotic behavior that is qualitatively similar to the previously-studied and presumable similar pinball and billiard systems [3,4,5]. The results are, instead, distinctly random in nature and small perturbations yield extremely divergent behavior beyond even the weak chaos of ergodic motion. This is due to the exponential divergence of two similar trajectories as they evolve in the system and because there is no attractor limiting (dissipating) that divergent behavior.

Ski-Slope Dynamics

Mogul field on a ski-slope

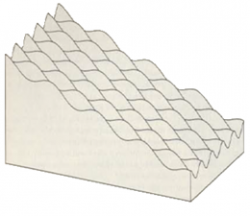
While Plinko as shown on the Price is Right is a random process, there are similar types of scenarios wherein an object descends through a regular field of obstructions that alter its trajectory as it descends. One such scenario is ski-slope dynamics [6]. In this scenario, a series of moguls are located on a slope, and a sliding object is allowed to descend under the force of gravity. As the sliding object interacts with the moguls, the trajectory is altered.

Lorenz created a simulation of this problem that shows significant chaotic behavior. Tracking cross slope velocity as a function of cross slope location for a variety of downslope positions shows the formation of an attractor, as shown in the image to the right. The peaks of the moguls are similar in nature to the pegs of the Plinko board, in that any object approaching the peak will tend to get repelled. However, instead of a discrete collision as exists within Plinko, a ski-slope provides continuous force acting on the object. This serves to create a continuously varying trajectory which does not necessarily diverge from neighboring trajectories as was seen in Plinko. Lorenz provides a simulation which sets a framework for looking at ski-slope dynamics, but does not have experimental data to support the model.

Progression of attractor structure descending down the ski-slope

Experiment

Our experimental protocol consists of two parts. A physical modeling and analysis with a plinko board constructed of low cost material and simple point tracking with labview and Matlab. The second is a numerical simulation coded in Matlab to study the dynamics of the system upon simple changes in starting parameters and collision elasticity.

Physical model

The constructed plinko board will be built from low cost materials. Wood is an easy choice for the back of the board, while a clear plexiglass front will be necessary to track the path of a puck upon entering the lattice of pegs. A ping pong ball is chosen due to its low cost, and light weight. A notional diagram showing the setup of the experiment is seen in the figure.

Experimental setup

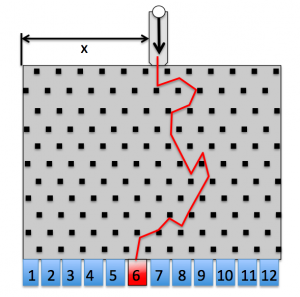
The experiment will be conducted by dropping the ball into the device from a known starting position. The end state will then be mapped to the starting position. The puck will be dropped from a position on a pre-determined grid using a device that drops the puck without imparting any initial velocity or rotation (such as a tube with a bottom that drops out). The physical experiment will be conducted on the order of 100 times to form a coarse grid for comparison with the numerical simulations. A more concentrated series of drops may also be performed in regions of rich chaotic dynamics to verify sensitivity shown in the numerical simulation.

<videoflash>Tmf18EciFQs</videoflash>

<videoflash>3o23-CVlYyA</videoflash>

Numerical simulation

The numerical simulation will be built in MATLAB and will use rigid body dynamics to simulate the collisions between the puck and the pegboard. The collisions will be modeled as elastic collisions with an optional parameter to modify the angle of reflection to produce modified, pinball-billiard dynamics (and thus create the possibility for attractors and more interesting dynamics, Markarian and Sanders). Using this simulation, we will model the physical layout of the Plinko board as shown in the figure.

The simulated Plinko model will be used to generate a finely-detailed mapping of initial position to final position. Final positions will be discrete bins that the puck may fall into. The initial position will be a combination of lateral starting position (distance from the static wall) and vertical position (speed at first peg impact). The numerical simulation will be run on the order of 1,000-10,000 times for both pure elastic and modified elastic collisions (based on run time) to calculate the mappings. Several values for the inelastic damping constant will be used, from a very small effect to a large effect on angle of reflection of the puck.

Analysis of Results

Analysis of the results will compare the two assumptions used in numerical simulation (elastic and modified elastic collisions) with the results of the physical trials in order to validate and compare numerical models, and to create a map of the initial state to the final state. A comparison between the results from the physics-based simulation and the traditional, probabilistic model will be performed, with special emphasis on looking at how multiple computer runs from different starting heights effects aggregate results and on the similarity between the deterministically-calculated trajectories and the probabilistic trajectories.

References

[1] http://phet.colorado.edu/en/simulation/plinko-probability. Plinko Probability. University of Colorado Active Simulations.

[2] Biesterfeld, A. “The Price (or Probability) Is Right.” University of Colorado at Boulder. Journal of Statistics Education. Volume 9, Number 3 (2001).

[3] Pring, S. R. Budd, C. J. “The Dynamics of a Simplified Pinball Machine.” University of Bath. IMA Journal of Applied Mathematics. 2011.

[4] Markarian, R. Pujals, E. J. Sambarino, M. “Pinball Billiards with Dominated Splitting.” Ergod. Th. & Dynam. Sys. Cambridge University Press. 2010.

[5] Arroyo, A. Markarian, R. Sanders, D. P. “Bifurcations of Periodic and Chaotic Attractors in Pinball Billiards with Focusing Boundaries.” Nonlinearity. IOP Publishing. 2009.

[6] Lorenz, E. "The Essence of Chaos." The Jessie and John Danz Lectures. UCL Press, 1995.