Group 1: Difference between revisions
| Line 11: | Line 11: | ||
== Background Theory == | == Background Theory == | ||
The formation of Faraday waves has been studied in several physical context, including convective fluids, nematic liquid crystals, nonlinear optics, biology, and, recently, in Bose-Einstein condensates; where the mechanisms of pattern selection was investigated using the tools of symmetry and bifurcation theory. Faraday waves in Non-Newtonian fluid was also recently studied. It was found that it is possible for holes to be created inside fluids such as cornstarch when undergoing vertical oscillation. Forming at a critical driving shaker acceleration and frequency, these holes are unusual in that their motion is not directly dependent on the Faraday waves, because the holes form far away from each other in the medium and tend to merge if they get to close to each other. Zhang and Vi\~nals have derived and equation that describe Faraday-wave amplitudes in the weakly damped and infinite depth limit. These equation has been tested in the weakly viscous and large depth limit and it provides a good agreement between this theory and experiments under these conditions. This theory predicts that the preferred patterns are the ones in which the Lyaupunov functional is minimized; which predicts for most excitation frequencies a square pattern for low viscous fluids. But for a narrow frequency band, hexagons and other quasi-periodic patterns are predicted. | |||
The experimental observation are: at high viscous dissipation, the observed wave pattern above threshold consists of parallel stripes; at lower dissipation, patterns of square symmetry are observed in the capillary regime of large frequencies. At low frequencies, higher symmetry patterns have been observed like hexagonal, and eight- and ten-fold quasi-periodic patterns. However, many of the experiments use shallow viscous layers of fluid to counteract the presence of high frequency weakly damped modes that can make patterns hard to observe. (A map of patterns vs. frequency is know. Current research aims at the study of this nonlinear pattern formation at a finite distance from threshold. It is now known that the evolution of the wave pattern near onset is variational, and its parameter space behavior is small in most fluids and vanishes with the viscous damping parameter. Non-variational corrections are anticipated to be large near onset, and play a important role in Faraday-wave instabilities and on the transition to spatio temporal chaos. | |||
===Formula Pastebin=== | ===Formula Pastebin=== | ||
:<math>\nabla\cdot\mathbf{v} = 0</math> | :<math>\nabla\cdot\mathbf{v} = 0</math> | ||
Revision as of 10:06, 16 December 2011
Faraday Waves and Nonlinear Patterns
Group members: J. Orphee, P. Cardenas-Lizana, M. Lane, E. Grossman
Introduction
- Eponymously discovered by Faraday[1], Faraday Waves are standing waves on a fluid caused by vertical oscillatory motion. At given frequencies, these standing waves (vibrating at held the driving frequency) give surface patterns of n dimensional rotational symmetry; mainly square, hexagonal, and 8-fold quasi-static patterns. The wavelength of the standing waves are a function of viscosity, surface tension and density. Hence, understanding the relationship between these variables and the wavelength, will allow oscillation frequencies to be selected that produce standing waves of order n [2]:

a) n=2 (square symmetry) b) n=3 (hexagonal symmetry) c) n=4 (8-fold quasiperiodic) d) n=5 (10-fold quasiperiodic)
The principle in this experiment is to vibrate a container with liquid vertically at a fixed frequency and amplitude. These waves consist of a standing wave pattern that occurs in a free fluid surface under excitation. At low vibration amplitudes, the liquid moves as a solid body, but at high vibration amplitudes, surface waves start to form. For instance, When a layer of fluid is oscillated up and down with a sufficiently large amplitude, patterns form on the surface, a phenomenon first observed by Michael Faraday in 1831. The standing waves form a pattern on the surface because the amplitude of the excitation exceeds a critical value. The excitation number is defined as $(A-Ac)/Ac$, where the vibration amplitude is denoted by $A$, the onset amplitude for the waves is denoted by $Ac$. This excitation number will define the characteristic of the pattern formation.
A collection of different wave modes compete and which pattern wins depends on the excitation number, the frequency, and the liquid viscosity. It is worth noting that all the modes have the same wave length, and that the wave length is independent of the vibration amplitude. In addition, the patterns observed are approximately independent of the boundary conditions for large enough containers; however if the container is small, the shape of the boundary will interfere and may destroy the pattern formation. The patterns range from squares, hexagons, triangular, and 8-fold quasi-periodic depending on the excitation frequency fluid properties (viscosity, surface tension, and density) Even though this phenomenon has been studied since its discovery by Faraday, a full understanding of the subject has not yet emerged.
Background Theory
The formation of Faraday waves has been studied in several physical context, including convective fluids, nematic liquid crystals, nonlinear optics, biology, and, recently, in Bose-Einstein condensates; where the mechanisms of pattern selection was investigated using the tools of symmetry and bifurcation theory. Faraday waves in Non-Newtonian fluid was also recently studied. It was found that it is possible for holes to be created inside fluids such as cornstarch when undergoing vertical oscillation. Forming at a critical driving shaker acceleration and frequency, these holes are unusual in that their motion is not directly dependent on the Faraday waves, because the holes form far away from each other in the medium and tend to merge if they get to close to each other. Zhang and Vi\~nals have derived and equation that describe Faraday-wave amplitudes in the weakly damped and infinite depth limit. These equation has been tested in the weakly viscous and large depth limit and it provides a good agreement between this theory and experiments under these conditions. This theory predicts that the preferred patterns are the ones in which the Lyaupunov functional is minimized; which predicts for most excitation frequencies a square pattern for low viscous fluids. But for a narrow frequency band, hexagons and other quasi-periodic patterns are predicted. The experimental observation are: at high viscous dissipation, the observed wave pattern above threshold consists of parallel stripes; at lower dissipation, patterns of square symmetry are observed in the capillary regime of large frequencies. At low frequencies, higher symmetry patterns have been observed like hexagonal, and eight- and ten-fold quasi-periodic patterns. However, many of the experiments use shallow viscous layers of fluid to counteract the presence of high frequency weakly damped modes that can make patterns hard to observe. (A map of patterns vs. frequency is know. Current research aims at the study of this nonlinear pattern formation at a finite distance from threshold. It is now known that the evolution of the wave pattern near onset is variational, and its parameter space behavior is small in most fluids and vanishes with the viscous damping parameter. Non-variational corrections are anticipated to be large near onset, and play a important role in Faraday-wave instabilities and on the transition to spatio temporal chaos.
Formula Pastebin
- <math>\nabla\cdot\mathbf{v} = 0</math>
- <math>
\frac{\partial \vec{v}}{\partial t}+\vec{v}\cdot\nabla\vec{v}= -\nabla \rho + \frac{1}{\mathrm{Re}} \nabla\cdot \left(\nabla\vec{v} + \nabla\vec{v}^T \right)+ \frac{1}{Fr}F(cos(2\pi t)-1)\mathbf{j}</math>
Previous Experiments
Binks and van de Water [2] choose to examine the stability of faraday waves as a function of excitation frequency. The wavelength of each mode can be determined from the inviscid deep fluid dispersion relation: ![]() where:
where:
![]() (g is acceleration due to gravity, k is the wave number, and 2w is the excitation frequency)
(g is acceleration due to gravity, k is the wave number, and 2w is the excitation frequency)
![]() (alpha is the surface tension, and rho is the density)
(alpha is the surface tension, and rho is the density)
Furthermore, the theory of this experiment is only valid for gamma << 1 where gamma is
![]() , the inverse Reynolds number.
, the inverse Reynolds number.
With these values, Binks and Water varied the amplitude of the oscillations for different frequencies and plotted the stable points on a phase diagram. In between each stable standing wave was a mixture of both waveforms. These transitionary states were shown to be bicritical points. Peilong and Vinals [4] were able to select stable points as a function of driving frequency and viscosity and plot them in a graph as shown:
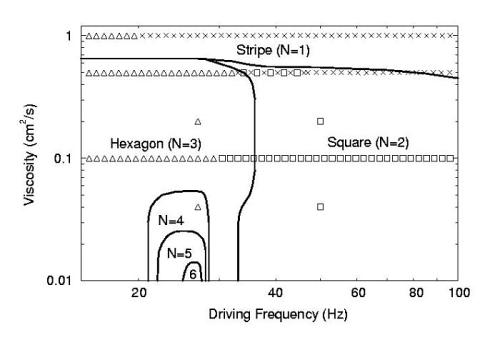
Non-Newtonian Fluid Experiments
Non-Newtonian fluids have the property that its viscosity is not constant as stress is applied to it over time. As the phase diagram below shows the higher viscosity, this means that the critical amplitude and frequency required for Faraday waves is higher and up to a point the number of possible Faraday waves will decrease or stop all together above certain of frequencies and amplitude. It is even possible for holes to be created inside fluids such as cornstarch when undergoing vertical oscillation (Goldman [7]). Forming at a critical driving shaker acceleration and frequency, these holes are unusual in that their motion is not directly dependent on the Faraday waves, because the holes form far away from each other in the medium and tend to merge if they get to close to each other. In fact the radius R(t) of a hole is depends on acceleration a, frequency f, and the resonant frequency of the material f0 by the formula:
- <math>
\begin{aligned} R(t) & = K * F(t+\varphi ) \\ F(t) & = Driving Function \\ \tan (\varphi ) & = \frac{\alpha }{1-\frac{f^2}{f_0^2}}\\ \end{aligned} </math> Instead Dr. Goldman and other’s found that it was the stability of these holes to last and remain open is dependent on the magnitude of the maximum shear thickening gamma, which is in turn affected by the viscosity eta and other proprieties of the liquid in question. In general the formula for shear thickening is:
- <math>
\begin{aligned} \eta & =\frac{2 \tau}{\pi \gamma ^{n-1} R(t)^3} & For Non-Newtonian \\ \eta & =\frac{2 \tau}{\pi \gamma R(t)^3} & For Newtonian \end{aligned} </math>
Experimental Setup
This experiment is designed to reproduce the results of quantifying the observance of these waves by Binks and W. van de Water [2]. The expected results should also agree with Zhang and Vinals' [3] prediction of the amplitudes of the standing waves. The experiment will go a step further and not only test the theory out for different fluids (including a non-newtonian fluid), but for different oscillatory patterns (square, sinusoidal,and triangle) .
Parts List
- Circular Cylinder
- High Speed CCD Camera
- 2 fluids with different viscosities (oils)
- A non newtonian fluid (cornstarch)
- An electromagnetic exciter (or any device that can oscillate vertically)
Procedure
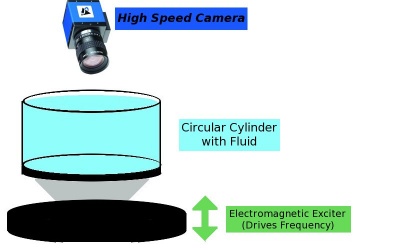
- Reproduce the experiments of Binks and Van de Water
- Fill a 440 mm diameter circular container with 20 mm height of experimental fluid
- Attach a 2 cm thick plate on the bottom of the container and a hollow conical structure attached to an electromagnetic exciter below that.
- Place piezo-electric accelerometers on the cone (one on bottom, two on top) to measure the acceleration cone. This allows control of the oscillation frequency.
- A high speed CCD camera is placed above the container to take snapshots of the standing waves. It is required that the frames per second of the snapshots are greater than the oscillation period of the standing waves.
- The amplitude of the oscillations are controlled by the electromagnetic exciter and increased in small steps (about 1%) where each wave is held for 2000 seconds first before taking 1000 s of images of the waves.
- Measurements of the amplitude of the waves are taken by a laser
- Compare the amplitudes and patterns with theory as a function of driving frequency
- Repeat experiment with another fluid, and a non newtonian fluid and checking if theory is consistent across different fluids.
- Observe the effects of changing the wave form on the standing waves
- Sinusoidal Waves
- Square Waves
- Triangle Waves
Visualization Of Faraday Waves
Results & Discussion
Newtonian And Non-Newtonian Fluid
Water is excited at 30Hz, and the forcing acceleration (the base shaking amplitude) is increased continuously from zero up to a maximum value, referred as the "ramp-up" in Figure \ref{Bif30Hz 2.jpg}. As the forcing acceleration increases, a critical acceleration is reached, (critical acceleration "up"), at which the Faraday waves start to form. At this critical acceleration "up" the wave amplitude exhibits a rapid increase with increasing forcing acceleration. If the forcing acceleration is increased further, the amplitude of the Faraday wave keeps increasing until the pattern becomes unstable. At this point, the input acceleration is decreased, "ramp-down", and the amplitude decreases back to zero. However, the "ramp-up" path and the "ramp-down" path are different, showing a hysteresis behaviour, as discussed in section \ref{Theoretical}. This hysteresis is consistent with a subcritical bifurcation, as depicted by the curve fit in Figure \ref{water30Hz}.
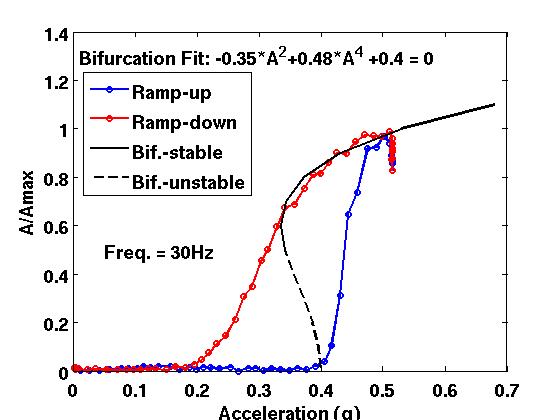 \caption{Normalized amplitude (amplitude/maximum amplitude) for water excited at 30Hz, for "ramp-up" path and "ramp-down" path, and corresponding bifurcation curve fit of the type: $0 = \epsilon -gx^2 -kx^4$.}
\label{water30Hz}
\end{center}
\end{figure}
The hysteresis and amplitude saturation arise due to a detuning effect of the natural frequency of the Faraday wave with respect to the excitation frequency. This detuning is caused by the fact that the natural frequency of the Faraday wave is a nonlinear function of its amplitude. Therefore, the natural frequency will be different for the case in which the amplitude is zero, acceleration increasing "ramp-up" path from rest, than when the amplitude is non zero, corresponding to a decrease in acceleration "ramp-down" path. The different natural frequencies means that the wave will be close or far from being in resonance with the forcing frequency. As the critical acceleration up is reached, the wave frequency response is in close proximity to being resonant; and thus, very unstable, with any perturbation causing the wave to form and increase in amplitude rapidly. However, as the amplitude grows, the natural frequency of the wave shifts away from resonance and the amplitude diminishes its growth rate, it saturates. This saturation is model by including a fifth order term in the amplitude equation, which balances the growth of the cubic term.
Similarly, the subcritical behaviour can be observed for a range of excitation frequencies 30-110Hz, as shown in Figure \ref{multiplefreq}, but the actual bifurcation shape will change for each frequency. For higher frequencies, the amplitudes and wavelengths become smaller. And for the highest frequency tested, 110Hz, the amplitudes are much smaller and the pattern becomes unstable.
The bifurcations have been fitted with equation \eqref{Phenomenological3}, and the fit coefficients are shown in Table \ref{fitcoeff}. As predicted by the theory for a subcritical bifurcation, $g < 0$ and $k > 0$. Where k is the coefficient of the fifth order term, which is stabilizing and responsible for modelling amplitude saturation. And $g < 0$, corresponds to the cubic, de-stabilizing, term.
Also, in order to explore the consistency of the particular bifurcation for each frequency, the experiment is repeated 5 times for each frequency, Figure \ref{multplefreqmultipletimes}. The general bifurcation shape is repeated, and thus there is a unique response of the fluid for a given excitation frequency. Also, there are approximate bounds for the critical accelerations "up" and "down".
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.3]{../Figures_Presentation/Bif_AllHz.jpg}
\caption{Normalized wave amplitude (amplitude/maximum amplitude) for water excited a 30-110Hz}
\label{multiplefreq}
\end{center}
\end{figure}
%
\begin{tabular}{|c|c|c|}
\hline
Frequency (Hz) & g & k \\
\hline
30 & -0.35 & 0.48 \\
\hline
40 & -0.94 & 1.8 \\
\hline
50 & -0.84 & 0.94 \\
\hline
60 & -1.6 & 3.1 \\
\hline
70 & -0.23 & 0.33 \\
\hline
80 & -0.25 & 0.27 \\
\hline
90 & -0.38 & 0.94 \\
\hline
110 & -0.006 & 1.2 \\
\hline
\hline
\label{fitcoeff}
\end{tabular}
%
%
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.4]{../Figures_Presentation/Bif_AllHzMultiple.jpg}
\caption{Normalized wave amplitude (amplitude/maximum amplitude) for water excited a 30-110Hz}
\label{multplefreqmultipletimes}
\end{center}
\end{figure}
Similarly, for the non-Newtonian fluid, the bifurcation behaviour is examined for a range of frequencies and compared with water, Figure \ref{watervscorn}. For the non-Newtonian fluid, the critical accelerations required are much higher due to a higher viscous dissipation, higher viscosity value as compared with water. Also, the shape of the bifurcation and its hysteresis are quite different as compared to water. For non-Newtonian fluids, the pattern may continue to exist for higher forcing accelerations, but its amplitude response shows a strong saturation, remaining almost flat, or in some cases even decreasing with increasing forcing acceleration.
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.3]{../Figures_Presentation/WaterVsNonNewt.jpg}
\caption{Normalized wave amplitude (amplitude/maximum amplitude) for Newtonian (water) and Non-Newtonian (mixture of water and cornstarch) excited a 30-110Hz}
\label{watervscorn}
\end{center}
\end{figure}
Since for a subcritical bifurcation, the system becomes unstable as the acceleration gets closer to the critical "acceleration up," a perturbation experiment is conducted, Figure \ref{taptest}. In this experiment, the container is physically tapped continuously as the acceleration is increased. As expected, the Faraday waves form before the critical acceleration up of the undisturbed system is reached. Also, as the acceleration is ramped down, the amplitude for the disturbed system reaches a critical "acceleration down" that is lower than the undisturbed system. This latter effect is surprising and may be due to the introduction of noise in the system which may widen the forcing frequency bandwidth, and increases the chances for the natural frequency of the Faraday wave to be closer to resonance with the forcing frequency, thus attenuating the amplitude decay with decreasing acceleration. This supposition is further reinforced by the next test, which compares a triangular wave input, with the base case, a sinusoidal input, Figure \ref{triangular}. The triangular wave in spectral space is composed on infinite number of wave numbers, and thus again this widens the forcing frequency spectrum; thus, increasing the chances that the natural frequency of the Faraday wave is tuned to some of the forcing wave numbers, and the amplitude decreases at a lower critical acceleration down. This same reasoning applies for the increasing amplitude case, which explains why the critical acceleration up happens before than for the sinusoidal input.
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.4]{../Figures_Presentation/Bif_Tap_60Hz.jpg}
\caption{Normalized wave amplitude (amplitude/maximum amplitude) for water excited a 60Hz for undisturbed system, and disturbed system ("Tap").}
\label{taptest}
\end{center}
\end{figure}
Furthermore, square wave inputs have been explored, but resulted in a wave pattern containing multiple wave numbers, Figure \ref{triangular}, and amplitude measurements become ambiguous.
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.15]{../Figures_Presentation/SinusoidalWave1.png}
\includegraphics[scale=0.15]{../Figures_Presentation/TriangularWave1.png}
\includegraphics[scale=0.15]{../Figures_Presentation/SquareWave1.png}
\caption{Faraday wave pattern for water excited a 60Hz for top to bottom: sinusoidal,triangular, and square forcing input wave form}
\label{triangular}
\end{center}
\end{figure}
The critical acceleration up and down as a function of frequency are shown for water and the cornstarch mixture in Figure \ref{criticalaccel}. As explained in the \ref{Theoretical} section, the critical acceleration increases with increasing frequency and viscosity due to the increase in dissipation at the boundaries of the container. And since in this experiment the viscosity of the non-Newtonian fluid is much higher than water, much higher critical accelerations are required to form a pattern.
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.5]{../Figures_Presentation/CriticalAccelVsFreq.jpg}
\caption{Critical acceleration for the ramp-up and ramp-down paths, for Newtonian (water) and non-Newtoninan (cornstarch mixture)}
\label{criticalaccel}
\end{center}
\end{figure}
The wavelength as a function of frequency for water and cornstarch mixture is also explored, Figure \ref{wavelength}, and compared with the theoretical approximation of $\lambda \sim {1/f}$ for shallow fluid depth. The results are in overall agreement with the theory, curve fits shown, for Newtonian and Non-Newtonian fluid.
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.5]{../Figures_Presentation/WavelengthVsFreq.jpg}
\caption{Wavelength as a function of forcing frequency for Newtonian (water) and non-Newtonian (cornstarch mixture)}
\label{wavelength}
\end{center}
\end{figure}
As mentioned, there is a maximum, saturated, amplitude for each forcing frequency, as shown in Figure \ref{MaxAmp}. While to the author there is no explicit theory that predicts the behaviour of the saturated amplitude versus forcing frequency, it seems that for larger frequencies $A_{max} \sim 1/f$. However, at 30Hz the maximum amplitude seems not to fit this approximation well, being surprisingly, about twice the amplitude of the 40Hz case, Figures \ref{MaxAmp} and \ref{sinusoidal}.
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.5]{../Figures_Presentation/MaxAmpVsFreq.jpg}
\caption{Maxiumu wave amplitude as a function of forcing frequency for Newtonian (water) fluid}
\label{MaxAmp}
\end{center}
\end{figure}
%
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.15]{../Figures_Presentation/30Hz_1.png}
\includegraphics[scale=0.15]{../Figures_Presentation/40Hz_1.png}
\includegraphics[scale=0.15]{../Figures_Presentation/110Hz_1.png}
\caption{Faraday waves at maximum amplitude for water excited at (from top to bottom):30Hz, 40Hz, and 110Hz}
\label{sinusoidal}
\end{center}
\end{figure}
Finally, the bifurcation departure of our experiment are compared in a qualitative manner with results from Wernet et al. \cite{wernet}, since experimental set-up and working fluids are different. Wernet et al. explored an amplitude departure for a working fluid with ~10 times the viscosity of water and the container used was carefully designed to avoid meniscus induced waves, "soft-beach" boundaries. Wernet et al. also tried to model the bifurcation without a fifth order saturating term; however, his work does not indicate whether this set-up induces a hysteresis behaviour. For the 60Hz, Wernet et al. shows a rapid increase of amplitude that resembles the sharp departure at "ramp-up" exhibited by water, Figure \ref{60Hz}. And at 80Hz, the results from Weret et al. show a slower departure from zero than water, but the cubic term amplitude departure (represented by the square root curve fit) seems not to agree well the amplitude saturation, which appears better captured with a fifth order term, shown by the subcritical bifurcation curve fit, Figure \ref{80Hz}.
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.5]{../Figures_Presentation/AmpVsReducedAcceleration60Hz.jpg}
\caption{Amplitude as a function of reduced acceleration $a/ac-1$ for water, and Wernet et al. working fluid for 60Hz excitation frequency}
\label{60Hz}
\end{center}
\end{figure}
%
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.5]{../Figures_Presentation/AmpVsReducedAcceleration80Hz.jpg}
\caption{Amplitude as a function of reduced acceleration $a/ac-1$ for water, and Wernet et al. working fluid for 80Hz excitation frequency}
\label{80Hz}
\end{center}
\end{figure}
\caption{Normalized amplitude (amplitude/maximum amplitude) for water excited at 30Hz, for "ramp-up" path and "ramp-down" path, and corresponding bifurcation curve fit of the type: $0 = \epsilon -gx^2 -kx^4$.}
\label{water30Hz}
\end{center}
\end{figure}
The hysteresis and amplitude saturation arise due to a detuning effect of the natural frequency of the Faraday wave with respect to the excitation frequency. This detuning is caused by the fact that the natural frequency of the Faraday wave is a nonlinear function of its amplitude. Therefore, the natural frequency will be different for the case in which the amplitude is zero, acceleration increasing "ramp-up" path from rest, than when the amplitude is non zero, corresponding to a decrease in acceleration "ramp-down" path. The different natural frequencies means that the wave will be close or far from being in resonance with the forcing frequency. As the critical acceleration up is reached, the wave frequency response is in close proximity to being resonant; and thus, very unstable, with any perturbation causing the wave to form and increase in amplitude rapidly. However, as the amplitude grows, the natural frequency of the wave shifts away from resonance and the amplitude diminishes its growth rate, it saturates. This saturation is model by including a fifth order term in the amplitude equation, which balances the growth of the cubic term.
Similarly, the subcritical behaviour can be observed for a range of excitation frequencies 30-110Hz, as shown in Figure \ref{multiplefreq}, but the actual bifurcation shape will change for each frequency. For higher frequencies, the amplitudes and wavelengths become smaller. And for the highest frequency tested, 110Hz, the amplitudes are much smaller and the pattern becomes unstable.
The bifurcations have been fitted with equation \eqref{Phenomenological3}, and the fit coefficients are shown in Table \ref{fitcoeff}. As predicted by the theory for a subcritical bifurcation, $g < 0$ and $k > 0$. Where k is the coefficient of the fifth order term, which is stabilizing and responsible for modelling amplitude saturation. And $g < 0$, corresponds to the cubic, de-stabilizing, term.
Also, in order to explore the consistency of the particular bifurcation for each frequency, the experiment is repeated 5 times for each frequency, Figure \ref{multplefreqmultipletimes}. The general bifurcation shape is repeated, and thus there is a unique response of the fluid for a given excitation frequency. Also, there are approximate bounds for the critical accelerations "up" and "down".
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.3]{../Figures_Presentation/Bif_AllHz.jpg}
\caption{Normalized wave amplitude (amplitude/maximum amplitude) for water excited a 30-110Hz}
\label{multiplefreq}
\end{center}
\end{figure}
%
\begin{tabular}{|c|c|c|}
\hline
Frequency (Hz) & g & k \\
\hline
30 & -0.35 & 0.48 \\
\hline
40 & -0.94 & 1.8 \\
\hline
50 & -0.84 & 0.94 \\
\hline
60 & -1.6 & 3.1 \\
\hline
70 & -0.23 & 0.33 \\
\hline
80 & -0.25 & 0.27 \\
\hline
90 & -0.38 & 0.94 \\
\hline
110 & -0.006 & 1.2 \\
\hline
\hline
\label{fitcoeff}
\end{tabular}
%
%
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.4]{../Figures_Presentation/Bif_AllHzMultiple.jpg}
\caption{Normalized wave amplitude (amplitude/maximum amplitude) for water excited a 30-110Hz}
\label{multplefreqmultipletimes}
\end{center}
\end{figure}
Similarly, for the non-Newtonian fluid, the bifurcation behaviour is examined for a range of frequencies and compared with water, Figure \ref{watervscorn}. For the non-Newtonian fluid, the critical accelerations required are much higher due to a higher viscous dissipation, higher viscosity value as compared with water. Also, the shape of the bifurcation and its hysteresis are quite different as compared to water. For non-Newtonian fluids, the pattern may continue to exist for higher forcing accelerations, but its amplitude response shows a strong saturation, remaining almost flat, or in some cases even decreasing with increasing forcing acceleration.
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.3]{../Figures_Presentation/WaterVsNonNewt.jpg}
\caption{Normalized wave amplitude (amplitude/maximum amplitude) for Newtonian (water) and Non-Newtonian (mixture of water and cornstarch) excited a 30-110Hz}
\label{watervscorn}
\end{center}
\end{figure}
Since for a subcritical bifurcation, the system becomes unstable as the acceleration gets closer to the critical "acceleration up," a perturbation experiment is conducted, Figure \ref{taptest}. In this experiment, the container is physically tapped continuously as the acceleration is increased. As expected, the Faraday waves form before the critical acceleration up of the undisturbed system is reached. Also, as the acceleration is ramped down, the amplitude for the disturbed system reaches a critical "acceleration down" that is lower than the undisturbed system. This latter effect is surprising and may be due to the introduction of noise in the system which may widen the forcing frequency bandwidth, and increases the chances for the natural frequency of the Faraday wave to be closer to resonance with the forcing frequency, thus attenuating the amplitude decay with decreasing acceleration. This supposition is further reinforced by the next test, which compares a triangular wave input, with the base case, a sinusoidal input, Figure \ref{triangular}. The triangular wave in spectral space is composed on infinite number of wave numbers, and thus again this widens the forcing frequency spectrum; thus, increasing the chances that the natural frequency of the Faraday wave is tuned to some of the forcing wave numbers, and the amplitude decreases at a lower critical acceleration down. This same reasoning applies for the increasing amplitude case, which explains why the critical acceleration up happens before than for the sinusoidal input.
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.4]{../Figures_Presentation/Bif_Tap_60Hz.jpg}
\caption{Normalized wave amplitude (amplitude/maximum amplitude) for water excited a 60Hz for undisturbed system, and disturbed system ("Tap").}
\label{taptest}
\end{center}
\end{figure}
Furthermore, square wave inputs have been explored, but resulted in a wave pattern containing multiple wave numbers, Figure \ref{triangular}, and amplitude measurements become ambiguous.
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.15]{../Figures_Presentation/SinusoidalWave1.png}
\includegraphics[scale=0.15]{../Figures_Presentation/TriangularWave1.png}
\includegraphics[scale=0.15]{../Figures_Presentation/SquareWave1.png}
\caption{Faraday wave pattern for water excited a 60Hz for top to bottom: sinusoidal,triangular, and square forcing input wave form}
\label{triangular}
\end{center}
\end{figure}
The critical acceleration up and down as a function of frequency are shown for water and the cornstarch mixture in Figure \ref{criticalaccel}. As explained in the \ref{Theoretical} section, the critical acceleration increases with increasing frequency and viscosity due to the increase in dissipation at the boundaries of the container. And since in this experiment the viscosity of the non-Newtonian fluid is much higher than water, much higher critical accelerations are required to form a pattern.
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.5]{../Figures_Presentation/CriticalAccelVsFreq.jpg}
\caption{Critical acceleration for the ramp-up and ramp-down paths, for Newtonian (water) and non-Newtoninan (cornstarch mixture)}
\label{criticalaccel}
\end{center}
\end{figure}
The wavelength as a function of frequency for water and cornstarch mixture is also explored, Figure \ref{wavelength}, and compared with the theoretical approximation of $\lambda \sim {1/f}$ for shallow fluid depth. The results are in overall agreement with the theory, curve fits shown, for Newtonian and Non-Newtonian fluid.
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.5]{../Figures_Presentation/WavelengthVsFreq.jpg}
\caption{Wavelength as a function of forcing frequency for Newtonian (water) and non-Newtonian (cornstarch mixture)}
\label{wavelength}
\end{center}
\end{figure}
As mentioned, there is a maximum, saturated, amplitude for each forcing frequency, as shown in Figure \ref{MaxAmp}. While to the author there is no explicit theory that predicts the behaviour of the saturated amplitude versus forcing frequency, it seems that for larger frequencies $A_{max} \sim 1/f$. However, at 30Hz the maximum amplitude seems not to fit this approximation well, being surprisingly, about twice the amplitude of the 40Hz case, Figures \ref{MaxAmp} and \ref{sinusoidal}.
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.5]{../Figures_Presentation/MaxAmpVsFreq.jpg}
\caption{Maxiumu wave amplitude as a function of forcing frequency for Newtonian (water) fluid}
\label{MaxAmp}
\end{center}
\end{figure}
%
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.15]{../Figures_Presentation/30Hz_1.png}
\includegraphics[scale=0.15]{../Figures_Presentation/40Hz_1.png}
\includegraphics[scale=0.15]{../Figures_Presentation/110Hz_1.png}
\caption{Faraday waves at maximum amplitude for water excited at (from top to bottom):30Hz, 40Hz, and 110Hz}
\label{sinusoidal}
\end{center}
\end{figure}
Finally, the bifurcation departure of our experiment are compared in a qualitative manner with results from Wernet et al. \cite{wernet}, since experimental set-up and working fluids are different. Wernet et al. explored an amplitude departure for a working fluid with ~10 times the viscosity of water and the container used was carefully designed to avoid meniscus induced waves, "soft-beach" boundaries. Wernet et al. also tried to model the bifurcation without a fifth order saturating term; however, his work does not indicate whether this set-up induces a hysteresis behaviour. For the 60Hz, Wernet et al. shows a rapid increase of amplitude that resembles the sharp departure at "ramp-up" exhibited by water, Figure \ref{60Hz}. And at 80Hz, the results from Weret et al. show a slower departure from zero than water, but the cubic term amplitude departure (represented by the square root curve fit) seems not to agree well the amplitude saturation, which appears better captured with a fifth order term, shown by the subcritical bifurcation curve fit, Figure \ref{80Hz}.
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.5]{../Figures_Presentation/AmpVsReducedAcceleration60Hz.jpg}
\caption{Amplitude as a function of reduced acceleration $a/ac-1$ for water, and Wernet et al. working fluid for 60Hz excitation frequency}
\label{60Hz}
\end{center}
\end{figure}
%
\begin{figure}[t]
\begin{center}
\includegraphics[scale=0.5]{../Figures_Presentation/AmpVsReducedAcceleration80Hz.jpg}
\caption{Amplitude as a function of reduced acceleration $a/ac-1$ for water, and Wernet et al. working fluid for 80Hz excitation frequency}
\label{80Hz}
\end{center}
\end{figure}
NonNewtonian Results
The intial plan for the Non-Newtonian part of our experiment was simply to measure and observe the similarities between the Non-Newtonian Faraday Waves and the Driving Signal Wave as well as observe the unique phenomena of holes and fingers that occur when on introduces a pertibation (see the video below). We decided to compare the bifurcation diagrams of Cornstarch to Water.
<videoflash>M_qXzyaIKI4</videoflash>
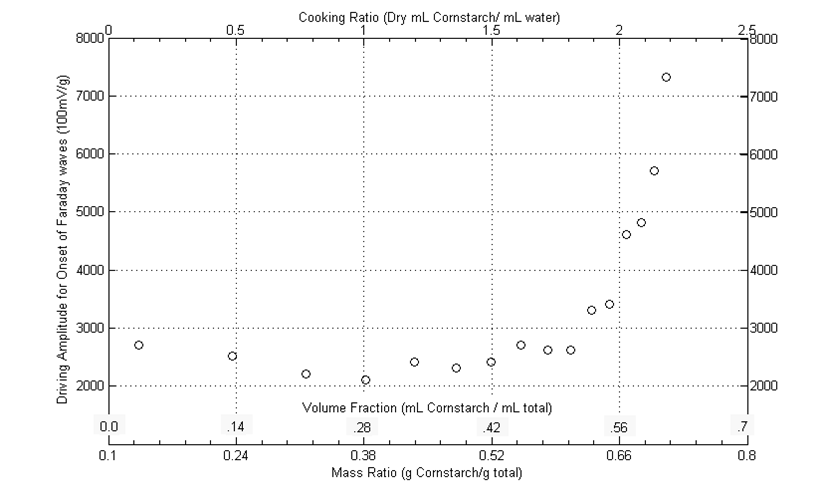 Early on we ran into an issue that there were a range of different values for the recipe and chemical properties of Non-Newtonian cornstarch mixture. Some researchers prefered to use Cornstarch with a oil while others simply used cornstarch and water. In fact, water mixed with cornstarch is a special Non-Newtonian called oobleck, coined by Dr. Suess. has an important role in teaching the physical chemstry for elementary school students. In order to figure out the ideal concintration we looked at how the upward onset of the Faraday instability bifurcation vs. concintration. As the figure above shows, the bifurcation asymptotically increases soon after a reciepe ratio of 2 parts cornstarch to 1 part water. For the rest of the experiment, we used a concintration of 2.5 : 1 since it seem to a fai upward bound.
Early on we ran into an issue that there were a range of different values for the recipe and chemical properties of Non-Newtonian cornstarch mixture. Some researchers prefered to use Cornstarch with a oil while others simply used cornstarch and water. In fact, water mixed with cornstarch is a special Non-Newtonian called oobleck, coined by Dr. Suess. has an important role in teaching the physical chemstry for elementary school students. In order to figure out the ideal concintration we looked at how the upward onset of the Faraday instability bifurcation vs. concintration. As the figure above shows, the bifurcation asymptotically increases soon after a reciepe ratio of 2 parts cornstarch to 1 part water. For the rest of the experiment, we used a concintration of 2.5 : 1 since it seem to a fai upward bound.
Conclusion
As the first video shows, we qualitatively observed holes and rising columns the unique pertibative properities. Above a critical acceleration, these holes remain persistant due to the thickening of the fluid. In fact the shearing pressure and strain of the pertibation causes water to dissolve out of the cornstarch solvent. As soon as the water is displaced, the free cornstarch molecules reform solid ionic bonds which then give the liquid it shear thickening properties.sd
Below is a video of the experiment we ran to measure the bifurcation for cornstarch.
<videoflash>IVxmY0CDF5g</videoflash>
In the video is abundantly clear that some cornstarch suspension is resists the driving amplitude and does not. In fact in some cases it seem like the solid-like layer of cornstarch was under the oscillating one. One theory for this inhomogenous boundary suggests that the inhomogenity is a result of the aging effects and packing of cornstarch as it is driven. Looking at the bifurcation diagrams we also see a jitter effect(*see N.J. Balmforth et al.) that causes an error in the parameter h/K that controls the vertical y(x=0) intial height of the bifurcation diagram.
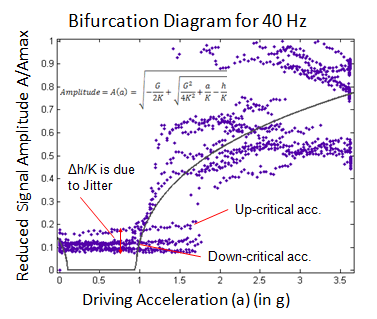
Newtonian vs. NonNewtonian
Other Captured Phenomena (Videos)=
This Lab
Other Labs
Faraday Waves on Cornflour
Faraday Waves set to music
Group Members
- Juan Orphee
- Paul Cardenas-Lizana
- Michael Lane
- Elan Grossman
Sources
- [1] M. Faraday, Philos. Trans. R. Soc. London 121, 319 (1831)
- [2] D. Binks and W. van de Water, Phy. Rev. Lett. 78, 4043 (1997) <http://alexandria.tue.nl/openaccess/Metis132530.pdf>
- [3] W. Zhang and J. Viñals, Phys. Rev. E 53, R4286 (1996)
- [4] Peilong Chen and J. Vinals, Phys. Rev. Lett, 79, 2670 (1997) <http://homepages.spa.umn.edu/~vinals/mss/peilong1.pdf>
- [5] J. Bechhoefer and B. Johnson, Am. J. Phys, 64, 12 (1996). <http://arxiv.org/pdf/patt-sol/9605002v1>
- [6] A. Kudrolli and J.P. Gollub, Physica D 97, 133 (1996)
- [7] Florian S. Merkt, Robert D. Deegan, Daniel I. Goldman, Erin C. Rericha and Harry L. Swinney, PRL 92, 184501 (2004) <https://www.physics.gatech.edu/files/u347/public/prl84501.pdf>