Group 3 2012

Chaos Circuits

Patrick Chang, Edward Coyle, John Parker, Majid Sodagar

Introduction

Chaos is aperiodic long-term behavior in a deterministic system that exhibits sensitive dependence on initial conditions [1]. Chaotic signals are usually broadband, noise like, and difficult to predict [2]. Therefore chaotic systems are suitable to carry information. In digital communication, sinusoidal carriers are used because they have optimal bandwidth efficiency and a relative ease of reconstruction of the original signal. However, their high power spectral density would cause a high level of interference and enhance the probability of interception by other receivers [3]. Chaotic carrier can solve this problem. A chaotic transmitter can send chaotic signal to the receiver, which synchronizes with the transmitter. Once synchronization is achieved, messages can be hidden in the chaotic signal and therefore be protected from unwanted interceptions [2]. Also, broadband information carriers enhance the robustness of communication and are less vulnerable to interference from narrow-band disturbance. This is the basis of spread-spectrum communication techniques, such as the code division multiple access (CDMA) protocol used in the Global Positioning System (GPS) and in the third generation of mobile telephones [4].

In order to achieve masking information in chaotic signal to obtain secure communication, the chaotic oscillators, transmitter and receiver, must be synchronized. In this experiment, we want to achieve synchronization between two or more Chua’s circuits acoustically [5] and study the dynamical behavior of the coupled oscillators with different media between the oscillators. Because Chua’s circuit is the simplest autonomous circuit that can exhibit bifurcations and chaos, it has been a very suitable subject for studying dynamical chaos by means of both laboratory experiments and computer simulations [5]. Acoustic coupling enables us to adjust various parameters to achieve synchronization, e.g. wave amplitude, feedback time delay, characteristic of media between the oscillators, etc. In the end, we want to find the condition and achieve oscillators’ synchronization in different environments.

Design and Parts

Chua's Circuit

Figure 1: Chua's Circuit

Figure 1 shows a typical Chua circuit. There are three main components to the circuit: the pair of capacitors, the inductor, and Chua's diode. Chua's diode is considered everything to the right of the C1 capacitor in Figure 1, and it is this part that causes the circuit to be nonlinear. Without this component, the circuit is a type of RLC circuit that will exhibit periodic behavior. The op-amp is used to drive the two diodes with a varying voltage. As the voltage varies, one of the diodes may cut off current going both ways if the voltage drops below the diode's cut-in voltage. This on/off behavior of the diodes drastically changes the circuit and causes chaotic behavior.

The design of our experiment will be rather simple. We will create multiple Chua circuits. We will construct each circuit to produce a chaotic signal, in terms of the voltages across two different capacitors and the current across an inductor. In Harada et. al's paper, two non-chaotic Chua circuits were coupled acoustically to produce a chaotic output. As a reverse of this experiment, we will couple two Chua circuits together using piezoelectric circuit parts, and will search for conditions in which the two Chua circuits produce a synchronized chaotic signal.

To produce this effect, we have multiple ways of altering the circuits. There will be variable resistors in each Chua circuit, the distance between the piezoelectric couplers can be varied, the medium between the piezoelectric couples can be changed in many ways, and we can even couple in a third Chua circuit, in parallel or series, if needed.

The data collection for all of this will be very simple. We will have an oscilloscope per Chua circuit, and we will compare between the two to see if they synchronize in any detectible fashion. The time frame for each phase of data collection is incredibly short, with usable results being produced in less than a second. This will allow us to go through a period of trial and error to discover if there is any set up of the circuit that would allow for non-chaotic behavior emerging from the coupling of chaotic Chua circuits.

The Equations

<math>\frac {dx}{dt} = α[y - x - g(x)]</math>

<math>\frac {dy}{dt} = x - y + z</math>

<math>\frac {dz}{dt} = -βy</math>

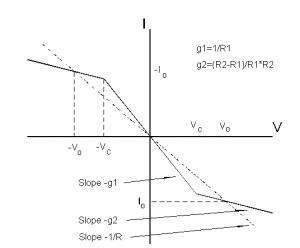
x(t) is the voltage across C1, y(t) is the voltage across C2, and z(t) is the current across L. α and β depend on the values of the various circuit components. The function g(x) is the source of the non-linearity, and it depends on the specifications of Chua's diode. The IV curve of a Chua's Diode is shown in Figure 2, and this is the piece-wise g(x) function used in the equations. For simulations of these equations, see references [1] and [4].

Figure 2: IV curve for Chua's Diode

Parts

• 3 - 10 nF Capacitors
• 3 – 100 nF Capacitors
• 3 – 15 mH Inductors
• 3 – Variable Resistors in kΩ range
• 6 – 220 Ω Resistors
• 6 – 22 kΩ Resistors
• 3 – 2.2 kΩ Resistors
• 3 – 3.3 kΩ Resistors
• 6 – MA23L3 Ultrasonic Transducers
• 3 – TL082

Procedure

Figure 3: A double scroll attractor

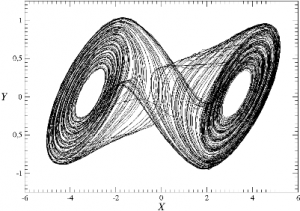
The first step in this experiment is to create a working Chua's circuit that exhibits chaotic behavior. This is measured using an oscilloscope. Chaos is achieved when the phase plane takes on a double scroll attractor, as shown in Figure 3. This can be achieved by varying the resistance of the resistor R in Figure 1. Once a Chua's circuit is successfully built, the circuit needs to be modified with an ultrasonic transducer so that the circuit produces acoustic output. Once again, chaos has to be achieved as measured by an oscilloscope. Once this is done, a duplicate will be made so that the two can become acoustically coupled. Measurements of the voltages inside both coupled circuits will be compared to see if there is any sort of synchronization.

References

Websites

    [1] http://crossgroup.caltech.edu/chaos_new/Chua.html
    [2] http://www.wellgainelectronics.com/muratama23l3.aspx
    [3] http://www.chuacircuits.com/
    [4] http://www.chuacircuits.com/sim.php
    [5] http://nonlinear.eecs.berkeley.edu/chaos/chaos.html

Literature

    [6] S. H. Strogatz, Nonlinear Dynamics and Chaos: With Applications To Physics, Biology, Chemistry, And Engineering (Studies in Nonlinearity). Westview Press, 2001, p. 512.
    [7] K. Cuomo, “Synchronization of Lorenz-based chaotic circuits with applications to communications,” Circuits and systems II: …, vol. 40, no. 10, pp. 626–633, 1993.
    [8] P. Arena, A. Buscarino, L. Fortuna, and M. Frasca, “Separation and synchronization of piecewise linear chaotic systems,” Physical Review E, vol. 74, no. 2, pp. 1–11, Aug. 2006.
    [9] A. Argyris, D. Syvridis, L. Larger, V. Annovazzi-Lodi, P. Colet, I. Fischer, J. García-Ojalvo, C. R. Mirasso, L. Pesquera, and K. A. Shore, “Chaos-based communications at high bit rates using commercial fibre-optic links.,” Nature, vol. 438, no. 7066, pp. 343–6, Nov. 2005.
    [10] Y. Harada, K. Masuda, and A. Ogawa, “Dynamical behavior of acoustically coupled chaos oscillators,” Fractals-an Interdisciplinary …, 1996.