Group 1 2014

Birds eye view of the experiment

Sedimentation of Chiral Particles in a Shear Flow

Group members: Johannes Jansson, Brian McMahon, Christian Reitz and Will Savoie

• Proposal presentation slides
• Whitepaper
• Project presentation slides
• Paper (not uploaded yet)

This is the website for the Chiral group. As a project for our Nonlinear Dynamics and Chaos class at Georgia Tech, we are investigating a method for the mechanical separation of chiral particles. The project is finished as far as this course concerns, but it will most likely result in more research and a more comprehensive paper. At the moment you can view our presentation material, whitepaper, actual paper, data, pictures and videos of our setup at this website.

Abstract

This experiment examines the separation of chiral particles via shear flow. We placed 3-D printed chiral particles in a high viscosity fluid and used a Taylor-Couette apparatus to generate a shear flow. The results of this experiment support research by M. Makino and M. Doi and give us a degree of insight into naturally occurring chiral behavior.

Motivation

Sorting particles based on their characteristics is a common goal in industrial and commercial applications. In chemistry, small differences in molecules can change their impact on the macroscopic scale. One such physical difference is chirality. The behavior of chiral particles is interesting due to their prevalence in biology. Chirality can also be important in the development of drugs, as enantiomers often have differing chemical properties. Shear flow may provide a mechanical separation method whereas most current methods are chemical. Such a method would be of interest to pharmaceutical companies because a mechanical method can prove to be cheaper and easier to perform. Our experiment will grant us a greater understanding of the physics that would be involved in such separation.

Theory

We consider a sheer flow, <math>\mathbf{v}(x,y,z) = \dot{\gamma}y\hat{x}</math>. Here, <math>\mathbf{v}</math> is the fluid velocity, <math>\dot{\gamma}</math> is the shear rate, and <math>\hat{x}</math> is the direction of shear flow, in this case a unit vector in the <math>x</math> direction. <math>y</math> represents a linear gradient of force in the <math>\hat{y}</math> direction (see Figure tk). We then consider a particle inserted into this flow:

<math>\left<{\mathbf{V}(t)}\right> = \mathbf{v} + \dot{\gamma}\left<\tilde{\mathbf{g}}\mathbf{N}\right></math>

<math>\mathbf{V}(t)</math> is the velocity of the particle, <math>\tilde{\mathbf{g}}</math> is a tensor encompassing the geometry and size of the particle, and <math>\mathbf{N}</math> is the direction of shear as it applies to particle geometry. Summarily, the particle's velocity is a sum of flow advection (<math>\mathbf{v}</math>) and motion due to the particle's geometry in concert with applied shear. One may also include a term for brownian motion <math>\mathbf{V_b}</math>, but the size of our particles was sufficiently large to make this term negligible. Due to the force gradient in <math>\hat{y}</math>, an inserted object experiences a torque about its <math>\hat{z}</math> axis. This rotation created by this torque may, depending on the geometry of the object, lead to motion in the <math>\hat{z}</math> direction. We can write this motion as:

<math>\left<V(z)\right> = \chi ga\dot{\gamma}</math>

Where <math>\chi = \{ 0,-1,1 \}</math> indicates the direction of the particle's chiraltiy, <math>g</math> is a constant based on particle geometry, and a is the particle size. We see that this is simply a reduction of the second equation to one dimension.

Method

To reach our goals for this experiment, we needed a highly viscous fluid in shear flow and, contained in the fluid, particles with of opposing chirality.

Figure 1: Sketch of a Taylor-Couette Device (courtesy of IOP Science)

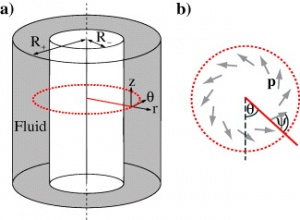
The centerpiece of the experiment was a Taylor-Couette device (figure 1). This device creates a reliable shear flow that should be optimal to see the separation effect. The velocity profile of the fluid is a direct result of the inner cylinder's spinning. There velocity will be maximum at the inner wall and drop off as a linear function of r. The boundary condition on the outer wall requires the velocity to go to zero. We designed our Taylor-Couette device in SolidWorks and printed all the parts except for the outer walls (that were constructed from transparent PVC tube) on a Makerbot Replicator.

The effect we are demonstrating has only been experimentally examined using rotating parallel plates before, this should be the first time the effect is demonstrated in Taylor-Couette flow. Since the separation effect depends on a high Peclet number, we will be using a highly viscous fluid. Our fluid of choice will be corn syrup, with a viscosity of 1450-2170. Finally, for chiral particles we went with a ribbon shape, similar to the ones used in the theory paper by Makino. They had a length of 10 mm, and were printed on the same 3-D printer as the Taylor-Couette device. The dowel was rotated using an ordinary cordless drill. The battery was disconnected and replaced by a power supply unit, so that we could control the velocity of the rotation by regulating the voltage.

Throughout this experiment we have chosen to use simple, easily accessible equipment. The Taylor-Couette device was rotated using a cordless drill, the video recording made using a smartphone. All other equipment was either 3-D printed or available at Publix or Home Depot.

Setup for the experiment

Figures

<videoflash>20H0hCYn1e0</videoflash>