Group 7

Group 7 page

The inverted pendulum is a simple mechanical system which models a canonical problem in both Control Theory and Nonlinear Dynamics. It is possible to control this system through either horizontal or vertical control of the pivot point. This article explores control of the planar pendulum through oscillation of the vertical position of the pivot point.

Background

The inverted pendulum with vertical driving has as it's Lagrangian

\begin{aligned}

    \mathcal{L} = \frac{m \ell^{2} }{2} \dot{\theta} ^{2} - m g \ell [1 - \cos(\theta) + y(t)] 

\end{aligned}

Where $\ell$ represents the length of the pendulum, $m$, it's mass, $\theta$ is the angle the pivot arm makes with the downward vertical, $g$ is the acceleration due to gravity, $y(t)$ is the vertical displacement of the pivot point, and $\dot{\theta}$ represents the derivative of the angle $\theta$ with respect to the time, $t$.

Solving the first-order Lagrange-Euler equation in $\theta, \dot{\theta}$ and rescaling, we find The Vertically Driven Pendulum equation

\begin{aligned}

   0 &= \ddot{ \theta} + (\alpha - \beta f(\tau)\theta \\
   \alpha &= \frac{g}{\ell \omega ^{2}} \\
   \beta &= \frac{b}{\ell} \\
   \tau &= \omega t \\

\end{aligned}

Where $f(\tau)$ corresponds to the normalized driving function, such that $ y(t) = b f(\tau)$, and $\ddot{\theta} $ is understood to be differentiated with respect to $\tau$, now.

Simulation

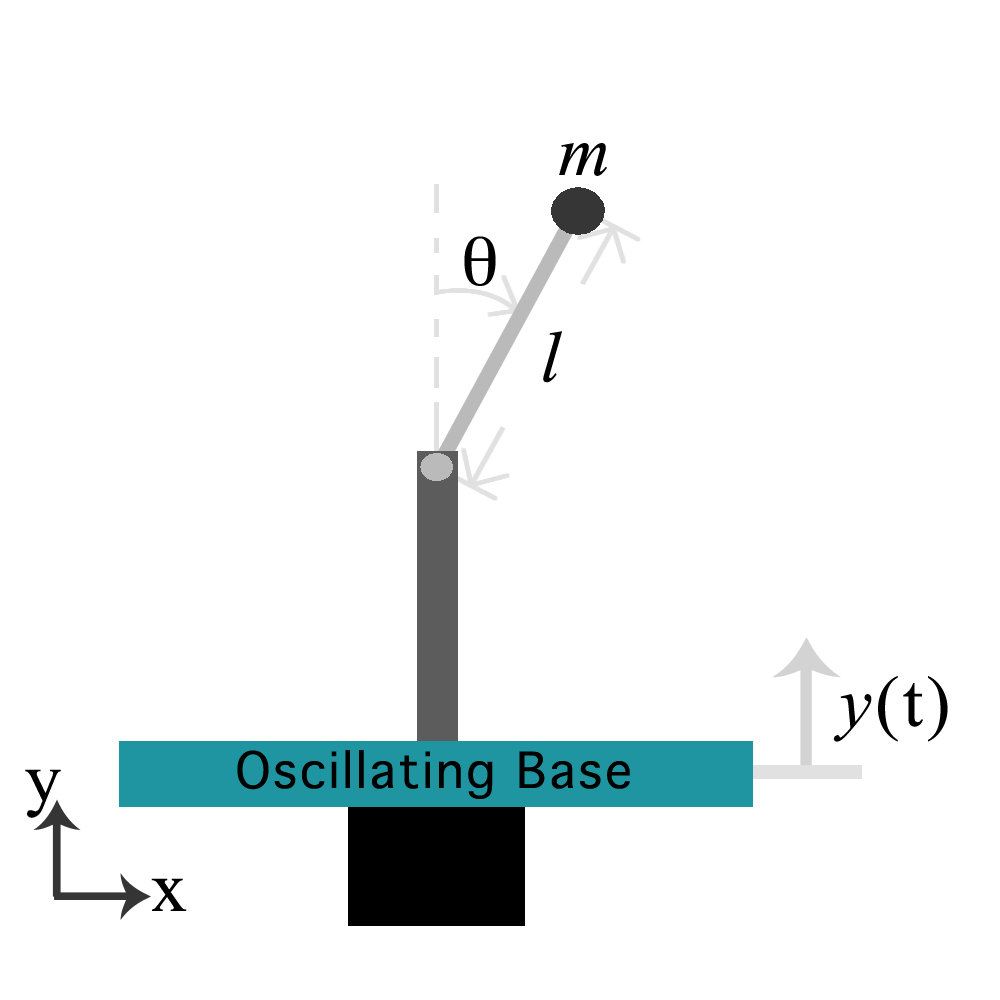A Matlab simulation was constructed in Simulink based on the single inverted pendulum with a vertically oscillating base.