Group 7: Difference between revisions
No edit summary |
No edit summary |
||
| Line 5: | Line 5: | ||
=== Background === | === Background === | ||
The inverted pendulum with vertical driving has as it's Lagrangian | The inverted pendulum with vertical driving has as it's Lagrangian | ||
\begin{equation} | \begin{equation} | ||
\mathcal{L} = \frac{m \ell^{2} }{2} \dot{\theta} ^{2} - m g \ell [1 - \cos(\theta) + y(t)] | \mathcal{L} = \frac{m \ell^{2} }{2} \dot{\theta} ^{2} - m g \ell [1 - \cos(\theta) + y(t)] | ||
\end{equation} | \end{equation} | ||
Where $\ell$ represents the length of the pendulum, $m$, it's mass, $\theta$ is the angle the pivot arm makes with the downward vertical, $g$ is the acceleration due to gravity, $y(t)$ is the vertical displacement of the pivot point, and $\dot{\theta}$ represents the derivative of the angle $\theta$ with respect to the time, $t$. | Where $\ell$ represents the length of the pendulum, $m$, it's mass, $\theta$ is the angle the pivot arm makes with the downward vertical, $g$ is the acceleration due to gravity, $y(t)$ is the vertical displacement of the pivot point, and $\dot{\theta}$ represents the derivative of the angle $\theta$ with respect to the time, $t$. | ||
Solving the first-order Lagrange-Euler equation in $\theta, \dot{\theta}$ and rescaling, we find The Vertically Driven Pendulum equation <ref> <\ref> | Solving the first-order Lagrange-Euler equation in $\theta, \dot{\theta}$ and rescaling, we find The Vertically Driven Pendulum equation <ref> <\ref> | ||
\begin{aligned} | \begin{aligned} | ||
0 &= \ddot{ \theta} + (\alpha - \beta f(\tau)\theta \\ | 0 &= \ddot{ \theta} + (\alpha - \beta f(\tau)\theta \\ | ||
| Line 21: | Line 21: | ||
\tau &= \omega t \\ | \tau &= \omega t \\ | ||
\end{aligned} | \end{aligned} | ||
Where $f(\tau)$ corresponds to the normalized driving function, such that $ y(t) = b f(\tau)$, and $\ddot{\theta} $ is understood to be differentiated with respect to $\tau$, now. | Where $f(\tau)$ corresponds to the normalized driving function, such that $ y(t) = b f(\tau)$, and $\ddot{\theta} $ is understood to be differentiated with respect to $\tau$, now. | ||
This simple second-order system can be generalized to include damping terms thus: | This simple second-order system can be generalized to include damping terms thus: | ||
\begin{equation} | \begin{equation} | ||
0 = \ddot{ \theta} + \gamma \dot{\theta} + (\alpha - \beta f(\tau)\theta | 0 = \ddot{ \theta} + \gamma \dot{\theta} + (\alpha - \beta f(\tau)\theta | ||
\end{equation} | \end{equation} | ||
Where $\gamma$ represents a constant, scaled, friction term. | Where $\gamma$ represents a constant, scaled, friction term. | ||
| Line 35: | Line 34: | ||
Through the use of a motor we attempt to force the stability of the free pendulum, such that the downward vertical ($\theta = 0$) becomes unstable and the upward vertical $(\theta = \pi$) becomes stable. | Through the use of a motor we attempt to force the stability of the free pendulum, such that the downward vertical ($\theta = 0$) becomes unstable and the upward vertical $(\theta = \pi$) becomes stable. | ||
== Materials == | == Materials == | ||
==Simulation== | |||
[[File:Diagram.png | thumb | 400px | alt = Diagram of the inverted pendulum]] | |||
Revision as of 20:39, 18 October 2011
Group 7 page
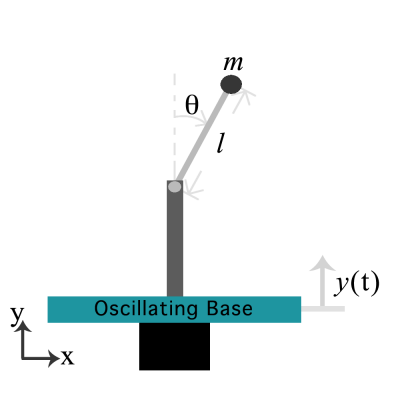
The inverted pendulum is a simple mechanical system which models a canonical problem in both Control Theory and Nonlinear Dynamics. It is possible to control this system through either horizontal or vertical control of the pivot point. This article explores control of the planar pendulum through oscillation of the vertical position of the pivot point.
Background
The inverted pendulum with vertical driving has as it's Lagrangian
\begin{equation}
\mathcal{L} = \frac{m \ell^{2} }{2} \dot{\theta} ^{2} - m g \ell [1 - \cos(\theta) + y(t)]
\end{equation}
Where $\ell$ represents the length of the pendulum, $m$, it's mass, $\theta$ is the angle the pivot arm makes with the downward vertical, $g$ is the acceleration due to gravity, $y(t)$ is the vertical displacement of the pivot point, and $\dot{\theta}$ represents the derivative of the angle $\theta$ with respect to the time, $t$.
Solving the first-order Lagrange-Euler equation in $\theta, \dot{\theta}$ and rescaling, we find The Vertically Driven Pendulum equation <ref> <\ref>
\begin{aligned}
0 &= \ddot{ \theta} + (\alpha - \beta f(\tau)\theta \\
\alpha &= \frac{g}{\ell \omega ^{2}} \\
\beta &= \frac{b}{\ell} \\
\tau &= \omega t \\
\end{aligned}
Where $f(\tau)$ corresponds to the normalized driving function, such that $ y(t) = b f(\tau)$, and $\ddot{\theta} $ is understood to be differentiated with respect to $\tau$, now. This simple second-order system can be generalized to include damping terms thus:
\begin{equation} 0 = \ddot{ \theta} + \gamma \dot{\theta} + (\alpha - \beta f(\tau)\theta \end{equation}
Where $\gamma$ represents a constant, scaled, friction term.
Experiment
Through the use of a motor we attempt to force the stability of the free pendulum, such that the downward vertical ($\theta = 0$) becomes unstable and the upward vertical $(\theta = \pi$) becomes stable.
Materials
Simulation