Group 4

Group Members: Luis Jover, Vlad Levenfeld, Brad Taylor, & Jeff Tithof

We plan to numerically and experimentally investigate the occurrence of and timescale for synchronization of up to $N=10$ coupled metronomes.

Background

The phenomenon of synchronization is found throughout nature and in many applications of different fields of science. Examples of synchronization include the flashing of firefly populations, the firing of pacemaker cells in the heart, applications of Josephson junctions, coupled fiber laser arrays, and perhaps even epileptic seizures. Many instances of synchronization in nature and applications in science become extremely complicated as soon as multiple variables or several coupled oscillators are introduced. However, the pervasive presence of synchronization in nature and science motivates work towards a deep understanding of such phenomena. So, as with any system that is to be scientifically understood, the simplest case is the best place to begin; for synchronization, the case of two identical, coupled oscillators is perhaps the simplest.

Research into the mutual synchonization of two identical coupled oscillators is believed to date back to the work of Christiaan Huygens in the 1600's, in which he discovered and investigated the synchronization of two pendulum clocks hanging on a common support beam. Although his goal was to solve the "Longitude Problem" at the time, he did reach some insightful conclusions about the nature of this system, eventually concluding that small movements of the support beam with every oscillation were responsible for the antiphase synchronization that consistently occurred.

Significant progress has been made in explaining simple instances of synchronization. In 2002, Bennett et al. <ref>M. Bennett, M. F. Schatz, H. Rockwood, and K. Wiesenfeld, ``Huygens's clocks," Proc. R. Soc. Lond. A 458, 563-579 (2002).</ref> constructed an apparatus meant to recreate the setup decribed by Christiaan Huygens. The experimental and numerical results agree qualitatively with records from Huygens's research. Concurrently, Pantaleone <ref>J. Pantaleone, ``Synchronization of metronomes," American Journal of Physics 70, 992-1000 (2002).</ref> investigated a similar setup in which metronomes were placed on a common support which was free to roll across cylinders, allowing coupling through the low-friction horizontal translation of the platform. Pantaleone's theoretical analysis provided agrees with the experimental observations reported.

In 2009, Ulrichs et al. <ref>H. Ulrichs, A. Mann, and U. Parlitz, ``Synchronization and chaotic dynamics of coupled mechanical metronomes," Chaos 19, 043120 (2009).</ref> reported agreement with Pantaleone's results in computer simulations. Additionally, these simulations were run for coupling of up to 100 metronomes and reportedly showed chaotic and hyperchaotic behavior. A paper by Borrero-Echeverry and Wiesenfeld <ref>Daniel Borrero-Echeverry and Kurt Wiesenfeld, ``Huygens (and Others) Revisted," Publication in progress, Obtained through personal contact (2011).</ref>, currently in the process of publication, describes a theoretical model which encompasses the behavior of both types of oscillators often studied, clocks and metronomes, which often contrast in the phase of synchronization encountered. This paper attributes the difference in synchronization phase to differences in parameters of the oscillators.

An arguably strong theoretical understanding of the $N=2$ case has been developed in recent years; it seems appropriate to expand this theory to a larger number of coupled oscillators. This is the goal of the current proposal.

Experiment

The experimental setup for the N=3 case. Note that this figure is not to scale.

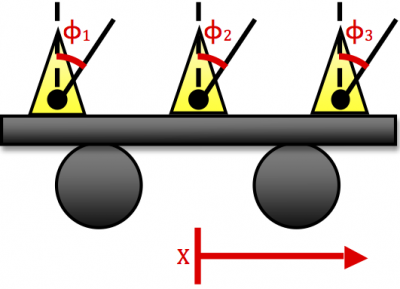
The figure to the right shows the experimental setup for the case of $N=3$. $N$ metronomes will be started with ``random" initial conditions and then placed on a rigid supporting platform, which will then be placed on top of two cylinders, allowing free horizontal translation. The translation of this platform is what provides the coupling between oscillators. Data will be collected through imaging the oscillations with a webcam and extracting the positions of each metronome as a function of time. A MATLAB script will quantitatively compare the phases and determine synchonization by criteria similar to that above. The occurrence, characteristics, and associated timescales for any synchronization encountered will be recorded. Experimental results will be compared to numerical results.

Below is a video of synchronization for $N=5$ from YouTube. <videoflash>Aaxw4zbULMs</videoflash>

Theory

The equations of motion for two coupled pendulums are available in Bennett et al.\cite{Bennett} and Wiesenfeld and Borrero-Echeverry\cite{Borrero}. These equations may easily be extended to $N$ metronomes:

\begin{equation} \label{dim_eq1} \ddot\phi_j+b\dot\phi_j+\frac{g}{l}\sin\phi_j=-\frac{1}{l}\ddot X \cos\phi_j+F_j\\ \end{equation}

\begin{equation} \label{dim_eq2} (M+m)\ddot X+B\dot X = -ml\frac{d^2}{dt^2}(\sin\phi_1+\sin\phi_2+ ... +\sin\phi_N) \end{equation} where $\phi$ is the angular displacement of the jth pendulum, $b$ is the pivot damping coefficient, $g$ is the acceleration due to gravity, $l$ is the pendulum length, $X$ is the linear displacement of the platform, $F$ is the impulsive drive, $M$ is the platform mass, $m$ is the metronome rod mass, $B$ is the platform friction coefficient, and the dots represent differentiation with respect to time.

Nondimensionalizing results in the following:

\begin{equation} \label{nondim_eq1} \frac{d^2\phi_j}{{d\tau}^2}+2\tilde\gamma\frac{d\phi_j}{d\tau}+\sin\phi_j=-\frac{d^2Y}{{d\tau}^2}\cos\phi_j+\tilde F_j\\ \end{equation}

\begin{equation} \label{nondim_eq2} \frac{d^2Y}{{d\tau}^2}+2\Gamma\frac{dY}{d\tau}=-\mu\frac{d^2}{d\tau^2}(\sin\phi_1+...+\sin\phi_N) \end{equation}

where we have introduced the dimensionless parameters:

\begin{equation} \label{nondim_param1} \tau=t\sqrt\frac{g}{l} \end{equation}

\begin{equation} \label{nondim_param2} \mu=\frac{m}{M+Nm} \end{equation}

\begin{equation} \label{nondim_param3} \tilde\gamma=b\sqrt\frac{l}{4g} \end{equation}

\begin{equation} \label{nondim_param4} \Gamma=\frac{B}{(M+Nm)}\sqrt\frac{l}{4g} \end{equation}

All parameters and variables described are well defined and may be experimentally measured, with the exception of $\tilde{F_j}$, the impulsive drive of the metronome, which receives a treatment first described in [1]. The escapement mechanism which ``kicks" the metronome is mimicked in two parts: first, the angular velocity of the pendulum is slowed by some factor $\gamma$, and then, a numerical constant $c$ is added to the angular velocity:

\begin{equation} \label{kick} \left|\frac{d\phi}{d\tau}\right|\to\gamma\left|\frac{d\phi}{d\tau}\right|+c \end{equation}

With a complete theoretical model, we must estimate the values of our parameters before we can fully construct a computer simulation of the experiment.

References

<references />