Group 3

Group members: Nitin Arora, Phillip Gray, Chris Rodesney, Jacob Yunis

Typical position of the ball (blue) and plate (black) versus time for c=3.

The appropriately-named bouncing inelastic ball experiment is composed of a perfectly inelastic ball bouncing on an oscillating plate. It is a simple yet elegant system that exhibits striking nonlinear behavior. On this page, we construct a computational model using various forcing waveforms for the plate, and generate associated bifurcation diagrams. We also explore experimentally the case of a harmonically forced plate.

Theory

The system of a ball bouncing completely inelastically on a vibrated platform has been the subject of numerous studies <ref>A. Mehta and J. M. Luck, Physical Review Letters 65, 393 (1990)</ref> <ref>T. Gilet, N. Vandewalle, and S. Dorbolo, Physical Review E 79, 055201(R) (2009)</ref>, and the case of a simple harmonically vibrated plate was completely resolved by Gilet et al. The primary means for analyzing the motion is measuring the time of flight between successive impacts of the ball with an n-cycle corresponding to the ball having n unique flight times before repeating. For small forcing, Gilet et al found an alternating series of one and two cycles with a small region containing an infinity of bifurcations around control parameter $\Gamma \simeq 7.253378$.

We investigate the case of a plate vibrated according to a superposition of two sine waves with a frequency ratio $c$:

<math> \begin{equation} x_p(t) = A[\sin(\omega t) + \sin(c \omega t)] \end{equation} </math>

The ball can take off from the plate when the acceleration of the plate is less than negative g, the acceleration due to gravity:

<math> \begin{align} \ddot{x}_p(t) = -A[\omega^2\sin(\omega t) + c^2 \omega^2\sin(c \omega t)] &\leq -g \notag\\ \frac{A\omega^2}{g} [\sin(\omega t) + c^2 \sin(c \omega t)] &\geq 1 \end{align} </math>

In this way, the motion of the ball from initial takeoff at <math>t_0</math> is:

<math> \begin{align} x_b(t) = &x_p(t_0) - x_p(t) + \dot{x}_p(t_0)(t-t_0) - 1/2 g(t-t_0)^2 \notag\\ x_b(t) = &A[\sin(\omega t_0)+ \sin(c \omega t_0) - \sin(\omega t) - \sin(c \omega t)] + A[\omega \cos(\omega t_0) + c \omega \cos(c \omega t_0)](t-t_0) - 1/2 g(t-t_0)^2 \notag \end{align} </math>

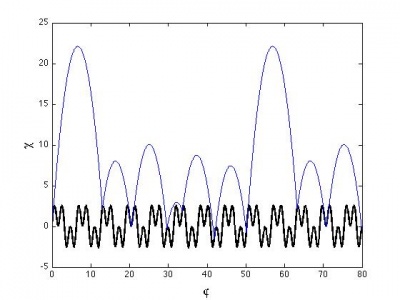
<math> \Gamma, \varphi, \chi</math> regime

The above functions can be made dimensionless via the introduction of a characteristic time <math>1/\omega</math> and a characteristic length <math>g/\omega^2</math>. We can thus define a phase <math>\varphi = \omega t</math>, a reduced acceleration and one of our control parameters <math>\Gamma = A\omega^2/g</math>, and a generalized position <math>\chi = A\omega^2/g</math>. The other control parameter is the ratio of the frequencies <math>c</math>.

The forcing of the plate is now given by:

<math> \begin{equation} \chi_p(\varphi) = \Gamma(\sin(\varphi) + \sin(c \varphi)) \end{equation} </math>

The position of the ball relative to the plate is

<math> \begin{align} \chi_b(\varphi) = &\Gamma[\sin(\varphi_0)+ \sin(c \varphi_0) - \sin(\varphi) - \sin(c \varphi)] + \dots \\ &\Gamma[\cos(\varphi_0) + c\cos(c \varphi_0)](\varphi - \varphi_0) - 1/2(\varphi-\varphi_0)^2. \notag \end{align} </math>

and the ball takes off when

<math> \begin{equation} \Gamma [\sin(\varphi) + c^2 \sin(c \varphi)] \geq 1 \end{equation} </math>

Period Doubling and Chaos

The flight time is defined as <math>T = \varphi_i - \varphi_0</math>, and can be found by solving the following equation numerically:

<math> \begin{align} F \equiv &\Gamma [\sin(\varphi_0)(1-\sin T) + \sin(c\varphi_0)(1-\sin cT) - \cos T \cos(\varphi_0) - \cos(cT)\cos(c\varphi_0)] - \dots \\

       &\Gamma[\cos(\varphi_0) + c\cos(c\varphi_0)]T - 1/2 T^2 = 0

\end{align} </math>

The ball is able to land in two distinct regions. There is a 'bouncing' region, where the acceleration of the plate is such that the ball will immediately take off again, with an initial velocity equal to the instantaneous velocity of the plate at the time of impact. The other region is the 'sticking' region, where the ball is not able take off, and instead rests on the plate until the plate's acceleration is such that is can take off again. This region is a sort of resetting region, as the ball immediately forgets any history it had prior to landing. The sticking region will mark the boundary between periodic cycles.

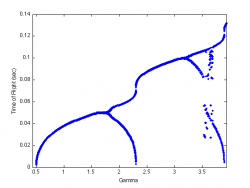
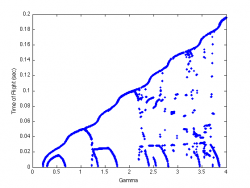
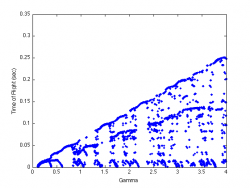
By varying the control parameter <math>\Gamma</math> we construct bifurcation diagrams for the cases <math>c=1, c=2</math> and <math>c=3</math>.

Bifurcation Diagrams

• 

  <math>c=1</math>

• 

  <math>c=2</math>

• 

  <math>c=3</math>

Parts list

1. oscilloscope or computer capable of outputting different forcing functions
2. shaker plate
3. completely inelastic hacky-sack type ball
4. high speed camera with computer interface
5. tracking software

Experimental Methods

In order to set up an inelastic bouncing ball system in the lab, we had to overcome 3 primary challenges: using a truly inelastic ball, constraining the ball to 1D motion, and accurately calculating the time of flight.

File:Iset.png

Initial setup

%

File:Fset.png

Final Setup

Initially, a sand filled bag on a driven plate surrounded by a plastic fence was used, see above. An accelerometer in the driven plate was used to calculate flight time. The input sine wave determined the takeoff point by calculating the takeoff line. The input sine wave was then subtracted out of the accelerometer signal to calculate the landing point. This signal was too noisy to be of use and the ball did not consistently remain in the center of the plate.

%

File:Accel.png

Noisy accelerometer signal

The lab setup was then reconfigured (see Final Setup above). A metal block (m = 249 g) with ball bearings was attached to a vertical pole to stabilize the motion in 1-D. This came at a cost of friction of the mass on the pole and slight elasticity of the mass. The friction was assumed to be Coulomb friction: constant with and opposite in sign to velocity. The friction was observed to be approximately 0.29 g. The takeoff times were calculated using an electrical circuit which was grounded at <math>x = 0 </math> The resulting signal provided very precise takeoff times.  The coefficient of restitution of the mass was observed to be <math>c_{R}\approx 0.515</math>.

Clean continuity signal

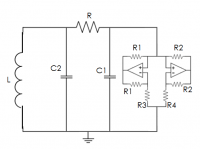
The friction was incorporated into the computational model developed in the Introduction, however the <math>c_{R}</math> was not, due to time constraints. Other experimental issues include the slight twisted of the mass due to nonuniform impact with the plate and low frequency shaker oscillation cause by feedback from the mass striking the plate at high <math>\Gamma</math>.

Data was collected at a sample rate of 20 KHz. The frequency of the plate was held constant during a run; the amplitude of the plate was altered to produce varying <math>\Gamma</math>. The frequency was varied between 20 and 40 Hz from run to run. The amplitude was stepped up gradually from <math>\Gamma=0</math> to <math>\Gamma=8</math> using a constant stepwise function. Different strategies were used to try to limit transients in the dynamics due to changing <math>\Gamma</math>. The optimal setup was to examine small ranges of <math>\Gamma</math> at a time, with between <math>50</math> and <math>100</math> oscillations at each <math>\Gamma<\math>. In addition, the first <math>10</math> oscillations at each $\Gamma$ thrown out to allow the system to settle.

%

File:Fric.png

Friction drop data

Results

To be found.

References

<references/>