Group 4 2012

Justin Blythe+ Yuxuan Jiang Section
Introduction
The reason that neighboring crickets tend to synchrony or a phase-lock is because of their mating habits. A sexually responsive female cricket is attracted to the chirp rhythm and the male cricket who tends to chirp in the lead<ref>Greenfield, M. D., & Roizen, I. (1993). Katydid synchronous chorusing is an evolutionarily stable outcome of female choice. Nature, (364), 618-620.</ref>. Thus the male crickets will slow down there chirp rate to synchronize with a preceding chirper or speed up it's chirp rate to synchronize with a quickly imitating chirp. A quantitative analysis of this phenomina was carried out by Thomas J. Walker in 1969<ref name="walker1969acoustic">Walker, T. J. (1969). Acoustic synchrony: two mechanisms in the snowy tree cricket. Science, (166), 891-894.</ref>. He found that an outside stimulus at a constant rate, which consisted of him holding a tape player, resulted in the neighboring crickets to synchronize with his recorded chirp.
We used this model to test both the biological accuracy of Stogatz's integrate-and-fire equation and to create an experimental procedure of this system. The equation that Strogatz and Mirollo gave was a spin-off of Peskin's model for self-synchronization of the cardiac pace-maker<ref name="mirollo1990synchronization">Mirollo, R. E., & Strogatz, S. H. (1990). Synchronization of pulse-coupled biological oscillators. 50(6), 1645-1662.</ref>.
\begin{equation} \frac{dx_i}{dt} = S_0 - \gamma x_i \end{equation}
Where $x_i$ is the state of an oscillator with $x_i \in [0,1]$, $S_0$ is a property of the oscillator in units of \emph{Hz}, and $\gamma$ is a dissipative term which gives the phase curve a concave down shape. Strogatz and Mirollo declared that this is a neccessary part for the integrate-and-fire model to synchronize, discussed more later. The criterion for synchrony is as follows,
\begin{equation} x_i = 1 \Rightarrow \; x_j(t^+) = \eta + x_j(t) \quad \forall j \neq i \end{equation} where $\eta$ is the associated coupling strength of the oscillator in question. This says that once one of the oscillators has fired the state of \emph{all} the other oscillators will be shifted by $\eta$.
To follow Walker's model for synchrony we had to modify how this equation was implemented. Instead of global synchrony, we use a lead and follow model where the leader does not shift it's chirp rate when the another cricket has chirped but the followers will. To account for outside noise, we added a time dependent noise term to the integrand. This is a common approach when dealing with noisy oscillators (cite noisy). Thus the resultant equation for our model is
\begin{equation} \label{eq:state2} \frac{dx_i}{dt} = S_0 - \gamma x_i + \zeta (t) \end{equation} \begin{equation} x_L = 1 \Rightarrow \; x_F(t^+) = \eta + x_F(t) \; \iff i=2 \end{equation} where $\zeta (t)$ is the external noise, $x_L$ is the state of the lead chirper, and $x_F$ is the state of the follower chirper.
Investigation of Pseudo-Synchronization in Crickets
Background
Alternation and Synchronization
There are many known species of insects, where signal interactions between males of the species result in neighboring males entering collective phase relationships, such as synchronizing (phase angle ≈ 0°) or alternating (phase angle ≈ 180°). Signal interactions, in this instance, are defined as phase adjustments a male makes to its sexual advertisement call, in response to other males <ref name="greenfield1994synchronous">Greenfield, M. D. (1994). Synchronous and alternating choruses in insects and anurans: common mechanisms and diverse functions. American Zoologist,34(6), 605-615. </ref>. This phenomenon has been well studied in choruses of crickets <ref name="hartbauer2005mechanisms">Hartbauer, M., Krautzer, S., Steiner, K., & Römer, H. (2005). Mechanisms for synchrony and alternation in song interactions of the bushcricket mecopoda elongate (tettigoniidae: Orthoptera). J Comp Physiol A, (191), 175-188. </ref><ref name="jones1966acoustic">Jones, M. D. R. (1966). The acoustic behaviour of the bush cricket Pholidoptera griseoaptera I. Alternation, synchronism and rivalry between males. Journal of Experimental Biology, 45(1), 15-30. </ref><ref name="walker1969acoustic">Walker, T. J. (1969). Acoustic synchrony: two mechanisms in the snowy tree cricket. Science, (166), 891-894.</ref>, Katydid calls <ref>Greenfield, M. D., & Roizen, I. (1993). Katydid synchronous chorusing is an evolutionarily stable outcome of female choice. Nature, (364), 618-620.</ref>, and the flashing of fireflies <ref>Buck, J. (1988). Synchronous rhythmic flashing of fireflies. II. Quarterly Review of Biology, 265-289. </ref>.
The general behaviors of synchronization and alternation in insects has been attributed to the mating preferences of females of the species. Where antecedent studies have shown that, when in the presence of pairs of synchronizing males, females show preference to the male whose signal leads most often <ref name="greenfield1994synchronous" />. Other evolutionary explanations for these phenomenon include the preservation of species-specific temporal patterns <ref name="walker1969acoustic" />, and the concealment of calls as a response to acoustically orientated predators <ref>Otte, D. (1977). Communication in Orthoptera. How animals communicate, 334-361. </ref>.
The majority of mathematical models describing this type of behavior do so by viewing the insects as coupled biological oscillators, which follow a phase response curve <ref name="greenfield1994synchronous" /><ref name="mirollo1990synchronization">Mirollo, R. E., & Strogatz, S. H. (1990). Synchronization of pulse-coupled biological oscillators. 50(6), 1645-1662.</ref>. Males will compete for the lead position in the chorus by shifting their position on the phase response curve slightly, resulting in them firing sooner and chirping, and, if successful, taking the lead <ref name="mirollo1990synchronization" />.
The Peculiar Behavior of Pholidoptera griseoptera
One species, which exhibits a very unique relationship arising from signal interactions, is Pholidoptera griseoptera, the dark bush cricket. When within proximity, males of this species will alternate their chirps, then synchronize for several iterations, before alternating once again <ref name="jones1966acoustic" />. The stage of synchrony observed is not perfect however; analysis of choruses has shown that there is always a partial overlap of the signals. In the case of two crickets, one will always be slightly leading the other in time <ref name="hartbauer2005mechanisms" />. This has been termed pseudo-synchronization (P-S), as audibly, it appears to be synchronization between the two crickets.

This complex behavior currently cannot be described according to models using a basic phase-response curve. The closest that a phase response model can come, is through phase drift, where a phase difference between two crickets signal rates would result in their signals gradually overlapping before moving apart again. However, there are two observations about the bush crickets behavior, which refute this as mere phase drift phenomena. First of all, as observed by Jones <ref name="jones1966acoustic" />, the shift from alternation to synchronization, between two crickets, is done in clearly discrete steps, not smoothly as would be expected if this was due to phase drift. Secondly, the amount of chirps for which the two crickets synchronize is highly variable, as opposed to the stable number we would expect from phase drift - over a 4 minute period, Jones was able to observe anywhere between 1 to 6 chirps per synchrony for the same two crickets <ref name="jones1966acoustic" />.
The data collected in Jones' research also brings forth another significant feature of the P-S behavior. Looking at two crickets of similar chirp rate, which have just undergone a synchrony event, it can be seen that the lead position always switches between crickets after such an event.
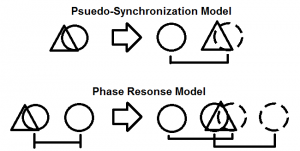
The Pseudo-Synchronization Model
The culmination of this information lends to the idea of a model in which crickets seem to carefully calculate their moves while attempting to overtake the lead position in the chorus. There are several inherent features of this type of model, which pose significant evolutionary advantages for a cricket. First of all, a cricket can more reliably gain the lead position in this model, as opposed to a basic phase response model, as it isn't sporadically shifting it's phase either up or down in the chance of taking the lead. It is making a calculated move into a P-S state, and then shifting forward into the lead. The second major advantage for a cricket following this type of model, is that when it does take the lead in this model, it will be by a maximum phase shift of roughly 180°. In the basic phase response model, there is a maximum phase shift which can be achieved if a cricket were to start from a position near P-S. However, in most cases, a cricket following a phase response model will not start from this ideal position, but in a range of unideal positions.
Methodology
Due to the fact that a mathematical model accurately describing the P-S behavior does not yet exist, data from live Pholidoptera griseoptera was analyzed in order to determine the favorability. In Jones' data of live cricket interactions, he notes the total duration of a recording,

the chirp rate of each cricket, the number of times a synchrony occurs, as well as the length of the synchrony (in chirps). Using this information, the synchrony occurrence ratio for live crickets was determined, and, under the assumption that all synchrony events do in fact lead to lead-switches, used as a measure of the favorability.
In order to be able to compare crickets controlled by a P-S model to crickets controlled by an alternative phase response model, specialized electronic crickets (SynCricks) were used. Each SynCrick consists of a microphone and a speaker, routed through a dedicated sound card, which is controlled through Matlab, where the particular phase-response model is defined. For the purpose of this study, the phase response model for coupled biological oscillators, as described by Mirollo and Strogatz <ref name="mirollo1990synchronization" />, was used. It must be noted, that due to instabilities within Matlab while analyzing a live audio feed, the base chirp rate of the SynCricks had to be slowed to 1 chirp per 5 seconds, as opposed to a more natural 0.5-1 chirps per second.
For the data collection, two SynCricks were arranged in a master-slave relationship; the master was preordained as the leader and made to chirp at a constant rate, whereas the slave started ≈ 180° out of phase with the master, and was allowed to regain the lead, following whichever model it employed. The start time of each SynCricks chirp was recorded to an excel spreadsheet for later analysis. As with the live crickets, data from the SynCricks was used to find the lead-switch occurrence ratio, used as a measure of favorability.
Results
From the more than 90 minutes of Jones' recordings of Pholidoptera griseoptera, 594 synchrony events were analyzed and used to determine the lead-switch occurrence ratio. These recordings occurred over several temperatures, and because crickets vary their chirp rate with temperature <ref name="walker1969acoustic" />, this was accounted for in all calculations. The syncrony occurrnce ratio, and thus lead-switch ratio, for Jones' cricket recordings was found to be 0.088.
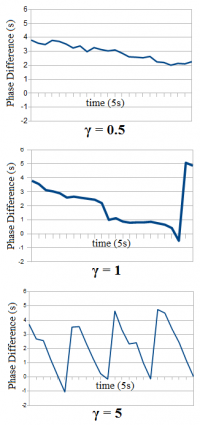
The model employed by the SynCricks allowed for a variable parameter of the coupling constant, so a range of realistic values of this constant were sampled and used to determine an average lead-switch ratio (FIG. 3). As with the live crickets, this data was used to find the measure of favorability of the behavior controlling model, in the form of the lead-switch ratio. This value was found to be 0.042 for the Mirollo-Strogatz phase response model.
The value of the lead-switch ratio is time independent, and thus should not be affected by the time scaling of the SynCricks chirp rate, for comparison purposes. In addition, there was a recorded 7% error between trials in Matlab, possibly due to the same reasons that required the chirp rate scaling.
Discussion and Conclusion
A comparison of the lead-switch ratios of the live crickets and the SynCricks, immediately poses a significant finding. The live crickets, assumed to be following the P-S model, had nearly double the lead-switch events within a sample than the SynCricks following a phase response model. Even accounting for the 7% error between trials, this result is significant in supporting the evolutionary favorability of a P-S model. This type of model allows crickets to fastidiously gain the lead position in a chorus, which thus increases their chances of attracting females and propagating their progeny.
However, this result leaves much room for further study of the P-S model. Determining the relative favorability of other, more advanced models of biological oscillators, would be necessary, as this research only tested one of the simplest cases. Possible such models include the Kuramoto phase response model, as well as oscillator timed automata <ref>Bartocci, E., Corradini, F., Merelli, E., & Tesei, L. (2009). Model checking biological oscillators. Electronic Notes in Theoretical Computer Science, 229(1), 41-58.</ref>. Another point of interest would be obtaining the mathematical formulation of the P-S model, which would require the collection of more data from live bush crickets; both to increase Jones' original sample size, as well as to get chirp interactions at a higher time resolution than was available to Jones in 1966.