Group 1 2012: Difference between revisions
Group4 2012 (talk | contribs) No edit summary |
Group4 2012 (talk | contribs) No edit summary |
||
| Line 33: | Line 33: | ||
== Poincaré section of the oscillator == | == Poincaré section of the oscillator == | ||
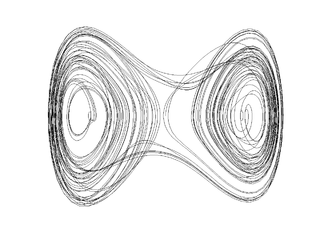
The Poincaré section is obtained by plotting <math>(x(t),y(t))</math> whenever ''t'' is a multiple of <math>\frac{2\pi}{\omega}</math>. This is the same thing as sampling the system at the same phase in every cycle. The Poincaré section for this system shows how the points fall on a fractal set and is very sensitive to initial conditions indicating the possibility of sustained chaos in the experiment. The Poincaré sections at low ''f'' is topologically equivalent to the sections at <math>f=0.</math> | The Poincaré section is obtained by plotting <math>(x(t),y(t))</math> whenever ''t'' is a multiple of <math>\frac{2\pi}{\omega}</math>. This is the same thing as sampling the system at the same phase in every cycle. The Poincaré section for this system shows how the points fall on a fractal set and is very sensitive to initial conditions indicating the possibility of sustained chaos in the experiment. The Poincaré sections at low ''f'' is topologically equivalent to the sections at <math>f=0.</math> In this case, the map has three fixed points and the stable and unstable manifolds do not intersect. As ''f'' increases, however, the stable and unstable manifolds become tangential and can intersect transversely. The creation of such a global homoclinic bifurcation leads to the presence of infinite transversal homoclinic orbits inidicating the presence of infinite number of unstable periodic orbits (of arbitrary periods). It also indicates the presence of bounded nonperiodic motion. All these together create the structure of the strange attractor. | ||
== Analog with the double well == | == Analog with the double well == | ||
Revision as of 11:10, 18 October 2012
Group members: Ross Granowski, Aemen Lodhi, Andrew Champion, Suchithra Ravi
Objective
The duffing oscillator is a simple model of a buckling beam which is subjected to lateral periodic forcing. Despite its simplicity, this system exhibits very rich dynamics and is now a classic example of chaos in a necessarily non-autonomous, two-dimensional system. We will attempt to capture the behavior of the system numerically and experimentally via Poincaré sections of trajectories in phase space. We will perform the same analysis with the cosine forcing term replaced by non-sinusoidal periodic functions.
Background
The Duffing oscillator is modeled by the following nonlinear, second-order, non-autonomous differential equation
for constants <math>\alpha,\beta,\delta,\omega,f>0</math>. Our goal in this experiment is to analyze bifurcations which occur for fixed <math>\alpha,\beta,\delta,\omega</math> as f is increased. It has been demonstrated numerically that period-doubling bifurcations and chaotic behavior occur in this case as well <ref name="VariousPeriodicForces" />. However, to the best of our knowledge, this has not been studied experimentally, and nothing has been written about the effect of alternate forcing functions upon the strange attractors in phase space which are observed in the sinusoidal case (although the case of small-amplitude forcing with general periodic functions was studied in <ref name="Morozov" />).
To begin to understand this equation, it is simplest to first analyze the case where <math>\delta=f=0</math>. In this case our equation reduces to
which is a Newtonian system with potential <math>V(x)= \frac{\beta }{4}x^{4}-\frac{\alpha}{2} x^{2}</math> and the trajectories are curves of constant energy <math>E(x,\dot{x})=\frac{1}{2}\dot{x}^{2}+V(x)</math>. In this case it is easy to see that we have a saddle at the origin and centers at <math>\left(\pm\sqrt{\frac{\alpha}{\beta}},0\right)</math>. Other than the two homoclinic orbits from the origin to itself and the two centers, we have that all other trajectories are in fact closed orbits.
Now when we include the dissipation term (i.e. we let <math>\delta>0</math>), the system is again easy to understand: heuristically, trajectories spiral into what are now stable fixed points at <math>\left(\pm\sqrt{\frac{\alpha}{\beta}},0\right)</math>. We can see that in this case
so the energy decreases (strictly, when <math>\dot{x}\neq 0</math>) along trajectories of the system. The origin is still a saddle in this case. It can be shown that, except for the stable manifolds of the saddle, all trajectories of this system tend toward one of the stable fixed points<ref name="Holmes" />.
The orbits become much more complicated for <math>f>0</math>. For small f, the behavior is well-understood (see <ref name="GuckenheimerHolmes" /> for details). In this case, the system closely resembles the non-forced system: the stable fixed points become attracting orbits of period <math>\frac{2\pi}{\omega}</math> and we still have something like a saddle near the origin. For large f, the behavior is also well-understood, since in this case the forcing term ``dominates" the other terms. In between these two extremes, the system becomes extremely complicated. In order to understand the behavior of the system with a ``mid-range" non-zero forcing term, <math>f>0</math>, its easier to study and analyze the Poincaré section of the trajectories.
Poincaré section of the oscillator
The Poincaré section is obtained by plotting <math>(x(t),y(t))</math> whenever t is a multiple of <math>\frac{2\pi}{\omega}</math>. This is the same thing as sampling the system at the same phase in every cycle. The Poincaré section for this system shows how the points fall on a fractal set and is very sensitive to initial conditions indicating the possibility of sustained chaos in the experiment. The Poincaré sections at low f is topologically equivalent to the sections at <math>f=0.</math> In this case, the map has three fixed points and the stable and unstable manifolds do not intersect. As f increases, however, the stable and unstable manifolds become tangential and can intersect transversely. The creation of such a global homoclinic bifurcation leads to the presence of infinite transversal homoclinic orbits inidicating the presence of infinite number of unstable periodic orbits (of arbitrary periods). It also indicates the presence of bounded nonperiodic motion. All these together create the structure of the strange attractor.
Analog with the double well
This system is analogous to a damped particle in a double well when the entire system is shaken. The two wells represent the two stable states of the buckled beam and the hump represents the saddle point when the beam is straight. When we apply a small force to one of the stable points, minor oscillations around the bottom of the well are produced. If a large force is applied, the particle is simply thrown from one well to the other. In the intermediate case (i.e., for forcing values in between) the particle may start out at the hump and chaotically move between the wells, because the particle falls one way or the other based on the timing and value of the forcing function as well as the particle’s energy.
Research questions
The scientific question we are trying to answer is whether different forcing functions produce qualitatively different chaotic behavior and bifurcations. Does the geometry of the strange attractor change based on the type of forcing function we use? Does the chaotic behavior persist for all kinds of forcing functions? These questions are important because existing literature has primarily focused on single cosine functions, but since this system is nonlinear, even a simple sum of cosines might lead to qualitatively different results. Real world signals typically contain noise or may have other forms (e.g., square or triangular). So, generalization of studies is possible only after we understand whether trajectories are completely different when the forcing functions are changed.
Experimental methods
We use the following experimental setup to explore the dynamics of the Duffing oscillator.
Electro-mechanical system concept
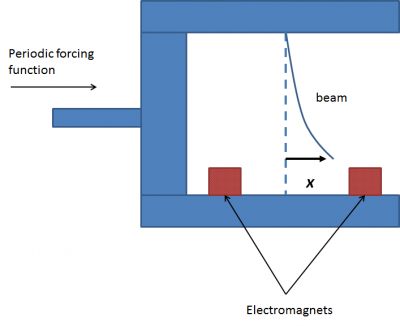
We attach a slender metallic beam to a rigid framework. Two electromagnets are attached at the base of the framework. The strength of the magnets is such that the metallic beam is pulled in the direction of one of magnets. Either configuration is stable. The position of the beam in the center is an unstable equilibrium as small disturbances to the framework cause the beam to buckle to one of the magnets. Since the goal of this experiment is to understand the forced vibration of the beam we apply an external force to the entire framework. Figure 1 gives the concept of the experimental setup.
Inputs and outputs
The following parameters will be provided as inputs to the experimental setup:
- Periodic forcing function frequency <math>\omega</math>
- Magnitude of the force <math>F</math>
- Strength of the electromagnet <math>E</math>
Superpositions of forcing functions and non-sinusoidal forcing functions, such as saw waves, will also be explored. The following signals will be measured as output from the experimental setup:
- The displacement of the metallic beam from the center position as a function of time <math>x(t)</math>
Physical setup
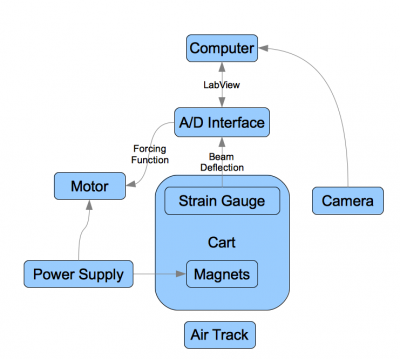
The physical setup of the experiment will consist of the following equipment, whose logical arrangement is shown in Figure 2:
- Air track and cart to act as the rigid framework shown in Figure 1
- Metallic beam, composed of shim stock with brass weights attached at the end as necessary to observe the desired dynamics
- Electromagnets
- Linear motor
- Signal generator for the forcing function
- Power supply
- Strain gauge to measure the displacement of the beam from the center. We will employ a strain gauge as well as a camera to record displacement in preliminary experiments to determine tradeoff in accuracy, sensor drift and computational complexity between the two methods. Visual measurements may require a large amount of computational storage space for long running experiments. Using a strain gauge may allow measurement of the curvature of the metallic beam while requiring less data storage and analysis. The strain gauge will be attached to a computer to record the displacement of the beam’s end from the center.
- A plexiglass setup to house the entire experimental setup (optional). We will measure the effect of air resistance on the experiment and if the effect is non-negligible we will house the entire experimental setup in a plexiglass case to isolate experiment.
Other factors such as air resistance, background magnetic fields, and loss of calibration of the strain gauge may impact experimental results and require modification of the experiment or sensor hardware.
Cost of experiment
We do not expect any costly procurements for this experiment. We expect that the equipment required to carry out this experiment will be available in any basic physics laboratory.
References
<references> <ref name="GuckenheimerHolmes">Guckenheimer, J. and P. Holmes (1983). Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer-Verlag.</ref> <ref name="Holmes">Holmes, P. (1979). A nonlinear oscillator with a strange attractor. Phil. Trans. R. Soc. Lond. A 292, 419–448.</ref> <ref name="Morozov">Morozov, A. (1973). Approach to a complete qualitative study of duffing’s equation. USSR Comput. Math. math. Phys. 13(5), 45–66.</ref> <ref name="VariousPeriodicForces">Ravichandran, V., V. Chinnathambi, and S. Rajasekar (2006). Effect of various periodic forces on duffing oscillator. Pramana 67(2), 351–356.</ref> </references>