Group 2 2012
Synchronization Breaking in Populations of Oscillating Fireflies
Group members: Ben McInroe, William Wagstaff, Mark Kingsbury, Morris Huang
Abstract
Firefly synchronization is a well-studied phenomena in nature that amends itself to models based on coupled oscillators. While many of these models have been mathematically proven to synchronize in the two oscillator case, and even the globally coupled case, it is not well understood whether groups of coupled oscillators synchronize if the topological connections between them are changed from global to local. In terms of fireflies, the fact that many fireflies remain grouped in trees or around bodies of water may be necessitated given the actual dynamics by which fireflies alter their internal frequencies. Our experimental results confirm this hypothesis by highlighting the ability of coupled oscillators to become saturated with information. By this, we mean that after a particular threshold of connections between fireflies, any additional connections do not reduce the time to synchronization. For fireflies, this means that the grouping behavior may be beneficial up to a critical point after which additional fireflies no longer aid in synchronization.
Background
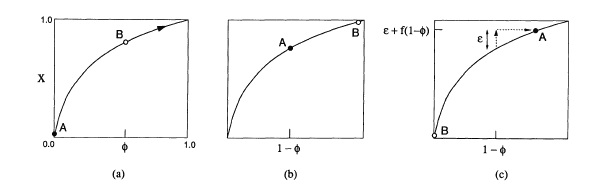
The flashing of fireflies is a familiar biological phenomenon that has been studied for hundreds of years \cite{ermentrout}. Its purpose is currently as a courtship behavior used during the mating season of the particular species, with usually mobile males flashing to signal typically stationary flashing females \cite{ermentrout}. As is the case for many biological oscillators, it has been observed \cite{buck} that when a population of fireflies flash in response to each other, coupling their dynamics, the characteristically nonlinear phenomenon of synchrony can occur, with the fireflies all flashing with identical frequencies. The exact biological and evolutionary advantages of this behavior are still a topic of debate among scientists, with several models proposed at the time of writing of this paper. Just as controversial is the question of which dynamical system best describes this behavior, with paths to synchronization proposed by Avila \cite{avila} and Ermentraut \cite{ermentrout}, and a general model for pulse coupled biological oscillators from Strogatz, which he has formally proven to produce synchrony for the case of N oscillators, for any positive integer N \cite{strogatz}. In this formulation, the oscillators are globally coupled and dynamically identical. Each firefly is assigned a state variable, x, such that $x=f(\phi)$, where $f:[0,1]\to[0,1]$ is smooth, increasing monotonically, and concave down. When the state $x_i$ of an oscillator reaches the threshold at 1, the state of each oscillator $x_j$ in the system is given a perturbation $\epsilon$ defined such that <math>x_j(t^+)=\min(1,x_j(t)+\epsilon)</math>.
<videoflash>a-Vy7NZTGos</videoflash>
(old background starts here)
There exist numerous models for the scenario of a population of flashing and synchronizing fireflies. The first of such models is proposed by Strogatz (cite):
Consider the scenario of a population of oscillators, each with identical parameters in amplitude and frequency, only distinguished by the their offset phases. Now, introduce another constraint, establishing that each oscillator is coupled equally to all others, regardless of their relative proximity. Under such conditions, global synchronization of the oscillators has a high probability of being achieved (Strogatz, Nature). This model can be applied to firefly synchronization, so long as the model caveats are satisfied. Specifically, the fireflies are assumed to be identical, have perfect line-of-sight of every other firefly, and are equally perturbed by nearby and distant flashes.
For characterizing our system of oscillators (fireflies), we will adopt the Peskin model for the cardiac pacemaker (cite Peskin paper), which is mathematically characterized by the following equation:
<math>\frac{dx_i}{dt} = S_0-\gamma x_i, \quad\quad\quad 0\leq x_i \leq 1, \quad\quad\quad i = 1, \dots ,N</math>
where $\gamma$ is the dissipation of the system, $S_0$ is the initial state velocity, and $x_i$ denotes the state for each oscillator in the global system.
An important characteristic of the state variable is that when $x_i = 1$, it fires and induces a state perturbation of $\epsilon$ on all other oscillators and subsequently drops back down to zero. This allows us to define $x_i$ as a periodic function dependent on its phase, or that $x = f(\phi)$. Under this definition, solving the above differential equation equation yields the following:
<math>f(\phi) = C(1-e^{-\gamma\phi})</math>
where $\phi$ is the phase of the oscillator and $C = 1-e^\gamma$.
Plotting this function and projecting the instantaneous states of a coupled two-oscillator system onto the graph (Figure 1) illustrates the fact that when the state of one oscillator (B) reaches threshold (X = 1), it is able to induce a phase shift on the other oscillator (A). By iterating this behavior, an entrainment will eventually be achieved between the two oscillators, or $\phi_A = \phi_B$.
Examining the function for the curve, it is important to note that when the system parameter $\gamma$ (dissipation) becomes large, the curve takes on a linear characteristic, which would prevent the phases of oscillators A and B from ever equating, as they remain phase-shifted at a fixed value for a linear function.
While this global system model does not incorporate any parameter that allows for a mathematical representation of communication-breakage between individual oscillators, we can develop this model parameter based on the experimental constraints we impose on our physical (and computational) model.
Another such model is the Kuramoto model >>>(KURAMOTO MATH GOES HERE)<<<
Experiment
For our experimental design, we will incorporate the use of a programmable LED board and camera. The LED board will enable us to define a specific set of LEDs as active, and these will start flashing based on randomized initial phase positions. The camera will serve as our sensor, capturing at a frame speed at least double of our LED flash frequency. In order to provide real-time adjustments to the LED's phases, the images will be processed in real-time LabVIEW and fed out by the LabVIEW digital output module to the LED board controller. This feedback loop will simulate the LED's "detecting" the surrounding flashes (through the camera) and phase-shifting according (through received digital output feedback).
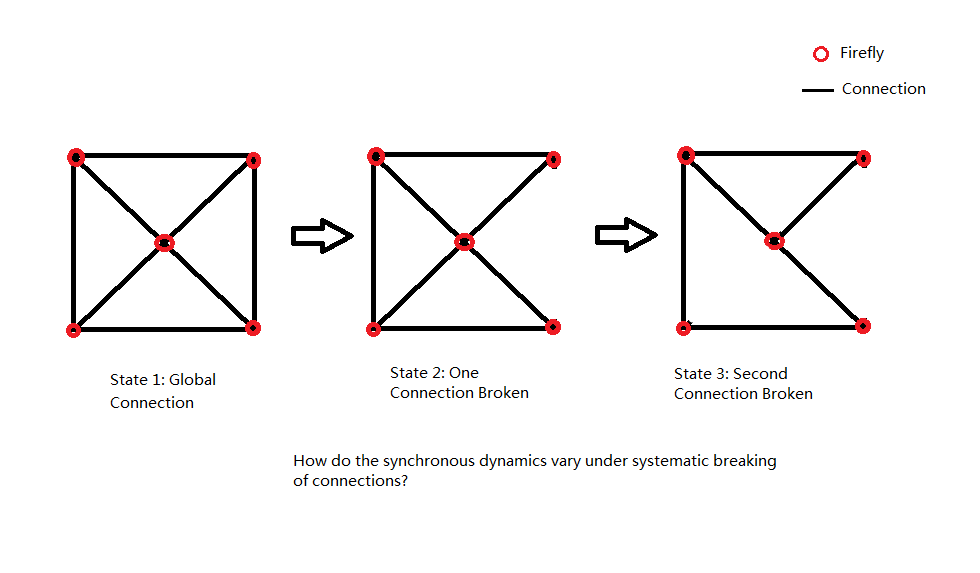
This real-time image processing methodology allows for a convenient means of defining constraining conditions for our array of LEDs (e.g. which inter-LED "connections" are broken). Utilizing this experimental methodology, we will attempt to find the "breaking point" of LED synchrony for the different scenarios of firefly couplings. The following is an example:
1) Given arrays of LEDs positioned as the vertices of different polygons, how many inter-LED connections can we break before global synchrony cannot be achieved consistently? We will impose the limitation that each LED, at most, will have only one of its connections broken.
2) For two equivalent sized families of LEDs where only one LED from each family can see each other, how large will the families need to be in order to consistently achieve local synchrony/stability such that they are unperturbed by the two inter-family LEDs? For a family, every LED included will be able to see every other LED within the same family.
Conclusion
Our project will examine how global synchronization breaking can occur in disjoint populations of oscillating fireflies through experimental means. It will be achieved by simulating networks of fireflies as LED lights in a network with physical boundaries and oscillator phase determined through the use of our high speed camera and computer program. Through these methods, we hope to better understand how variations in the network geometry of firefly populations can affect their ability to mutually synchronize.
Bibliography
Strogatz, S. H., Mirollo, R. E. Synchronization of Pulse-Coupled Biological Oscillators. SIAM Journal on Applied Mathematics. (50) 1645-1662.
Strogatz, S. H., Exploring Complex Networks. Nature (410) 268-276.
Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence (Springer, Berlin, 1984).
Winfree, A. T. The Geometry of Biological Time (Springer, New York, 1980).
Collins, J. J. & Stewart, I. Coupled nonlinear oscillators and the symmetries of animal gaits. J. Nonlin. Sci. 3, 349–392 (1993).