Group 6
Chua's circuit is a simple electronic circuit containing standard electrical components (resistors, capacitors, inductors, and an op-amp) developed by Leon Chua <ref>http://en.wikipedia.org/wiki/Leon_O._Chua</ref> that exhibits chaotic behavior.
Background
[type the background here]
Linear stability analysis
Chaotic dynamics
Experiment
Parts list
- Breadboard and jumper wires
- 5 100 ohm resistors (1/4 Watt)
- 3 20 picofarad capacitors
- 5 10 microhenry inductors
- 2 diodes
- 1 20V DC power supply
- 1 oscilloscope / DAQ
- 3 wire leads with alligator clips
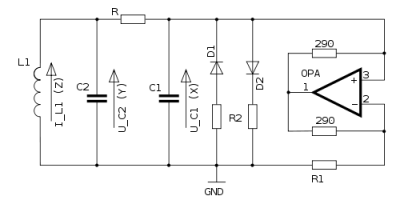
Using the Chua Circuit shown in Figure 4, the voltage waveforms v_{C_1} (t) and v_{C_2} (t) across capacitors C1 and C2, and the current waveform i_L (t) through the inductor L in Figure 1, were observed using an oscilloscope and displayed in Figure 5 (a), (b), and (c) (left column), respectively.
The Lissajous figures associated with 3 permutated pairs of waveforms are displayed on the right column Figure 5; namely, in the v_{C_1}-i_L plane in Figure 5(d), the v_{C_1}-v_{C_2} plane in Figure 5(e), and the v_{C_2}-i_L plane Figure 5(f). They are 2-dimensional projections of the chaotic attractor, called the double scroll, traced out by the 3 waveforms from the left column in the 3-dimensional v_{C_1} - v_{C_2} - i_L space.
It is important to point out that the Chua Circuit is not an analog computer. Rather it is a physical system where the voltage, current, and power associated with each of the 5 circuit elements in Figure 1 can be measured and observed on an oscilloscope, and where the power flow among the elements makes physical sense. In an analog computer (usually using Op Amps interconnected with other electronic components to mimic some prescribed set of differential equations), the measured voltages have no physical meanings because the corresponding currents and powers can not be identified, let alone measured, from the analog computer.
Simulation of Chua's circuit
Matlab code
The following code integrates the system of equations which model the circuit
<source lang="matlab"> % Models Initial Variables %-------------------------
TimeSeries = [x0, y0, z0]'; % models initial conditions
% Optimized Runge-Kutta Variables %--------------------------------
h = step_size*G/C2; h2 = (h)*(.5); h6 = (h)/(6);
anor = Ga/G; bnor = Gb/G; bnorplus1 = bnor + 1; alpha = C2/C1; beta = C2/(L*G*G); gammaloc = (R0*C2)/(L*G);
bh = beta*h; bh2 = beta*h2; ch = gammaloc*h; ch2 = gammaloc*h2; omch2 = 1 - ch2;
k1 = [0 0 0]'; k2 = [0 0 0]'; k3 = [0 0 0]'; k4 = [0 0 0]'; M = [0 0 0]';
% Calculate Time Series %----------------------
M(1) = TimeSeries(3)/E; M(2) = TimeSeries(2)/E; M(3) = TimeSeries(1)/(E*G);
for i=1:dataset_size
% Runge Kutta % Round One k1(1) = alpha*(M(2) - bnorplus1*M(1) - (.5)*(anor - bnor)*(abs(M(1) + 1) - abs(M(1) - 1))); k1(2) = M(1) - M(2) + M(3); k1(3) = -beta*M(2) - gammaloc*M(3); % Round Two temp = M(1) + h2*k1(1); k2(1) = alpha*(M(2) + h2*k1(2) - bnorplus1*temp - (.5)*(anor - bnor)*(abs(temp + 1) - abs(temp - 1))); k2(2) = k1(2) + h2*(k1(1) - k1(2) + k1(3)); k2(3) = omch2*k1(3) - bh2*k1(2); % Round Three temp = M(1) + h2*k2(1); k3(1) = alpha*(M(2) + h2*k2(2) - bnorplus1*temp - (.5)*(anor - bnor)*(abs(temp + 1) - abs(temp - 1))); k3(2) = k1(2) + h2*(k2(1) - k2(2) + k2(3)); k3(3) = k1(3) - bh2*k2(2) - ch2*k2(3); % Round Four temp = M(1) + h*k3(1); k4(1) = alpha*(M(2) + h*k3(2) - bnorplus1*temp - (.5)*(anor - bnor)*(abs(temp + 1) - abs(temp - 1))); k4(2) = k1(2) + h*(k3(1) - k3(2) + k3(3)); k4(3) = k1(3) - bh*k3(2) - ch*k3(3); M = M + (k1 + 2*k2 + 2*k3 + k4)*(h6); TimeSeries(3,i+1) = E*M(1); TimeSeries(2,i+1) = E*M(2); TimeSeries(1,i+1) = (E*G)*M(3); i=i+1;
end </source>
References
<references />