Group 2 2012: Difference between revisions
No edit summary |
No edit summary |
||
| Line 49: | Line 49: | ||
== Bibliography == | |||
== Bibliography == | |||
Strogatz, S. H., Mirollo, R. E. Synchronization of Pulse-Coupled Biological Oscillators. SIAM Journal on Applied Mathematics. (50) 1645-1662. | Strogatz, S. H., Mirollo, R. E. Synchronization of Pulse-Coupled Biological Oscillators. SIAM Journal on Applied Mathematics. (50) 1645-1662. | ||
Revision as of 02:46, 18 October 2012
Introduction
We are interested in studying the entrainment of pulse-coupled biological oscillators, specifically populations of fireflies. Many species of fireflies use bio-luminescent flashing to attract mates. When a group of fireflies flash together, each starting at arbitrary phases, natural observation indicates that over some finite time scale, they are likely to achieve entrainment, and synchronous oscillatory behavior will emerge. The mathematical foundation of such a system is developed thoroughly by Strogatz in (insert paper here). However, such a model does not account for the existence of natural barriers that may divide a system of fireflies into different populations that do not exhibit universal coupling. Therefore, with this premise in mind, we obtain our central question: "At what point of communication parameter variation will the fireflies be prevented from consistently achieving synchrony?"
(Photo here)
Background
Consider the scenario of a population of oscillators, each with identical parameters in amplitude and frequency, only distinguished by the their offset phases. Now, introduce another constraint, establishing that each oscillator is coupled equally to all others, regardless of their relative proximity. Under such conditions, global synchronization of the oscillators has a high probability of being achieved (Strogatz, Nature). This model can be applied to firefly synchronization, so long as the model caveats are satisfied. Specifically, the fireflies are assumed to be identical, have perfect line-of-sight of every other firefly, and are equally perturbed by nearby and distant flashes.
For characterizing our system of oscillators (fireflies), we will adopt the Peskin model for the cardiac pacemaker (cite Peskin paper), which is mathematically characterized by the following equation:
<math>\frac{dx_i}{dt} = S_0-\gamma x_i, \quad\quad\quad 0\leq x_i \leq 1, \quad\quad\quad i = 1, \dots ,N</math>
where $\gamma$ is the dissipation of the system, $S_0$ is the initial state velocity, and $x_i$ denotes the state for each oscillator in the global system.
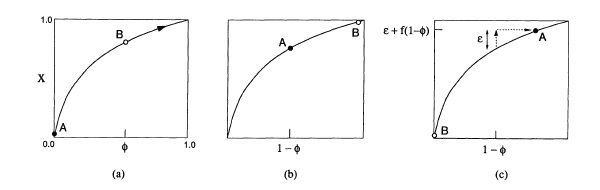
An important characteristic of the state variable is that when $x_i = 1$, it fires and induces a state perturbation of $\epsilon$ on all other oscillators and subsequently drops back down to zero. This allows us to define $x_i$ as a periodic function dependent on its phase, or that $x = f(\phi)$. Under this definition, solving the above differential equation equation yields the following:
<math>f(\phi) = C(1-e^{-\gamma\phi})</math>
where $\phi$ is the phase of the oscillator and $C = 1-e^\gamma$.
Plotting this function and projecting the instantaneous states of a coupled two-oscillator system onto the graph illustrates the fact that when the state of one oscillator (B) reaches threshold (X = 1), it is able to induce a phase shift on the other oscillator (A). By iterating this behavior, an entrainment will eventually be achieved between the two oscillators, or $\phi_A = \phi_B$.
Examining the function for the curve, it is important to note that when the system parameter $\gamma$ (dissipation) becomes large, the curve takes on a linear characteristic, which would prevent the phases of oscillators A and B from ever equating, as they remain phase-shifted at a fixed value for a linear function.
While this global system model does not incorporate any parameter that allows for a mathematical representation of communication-breakage between individual oscillators, we can develop this model parameter based on the experimental constraints we impose on our physical (and computational) model.
Experimental Details
For our experimental design, we will incorporate the use of a programmable LED board and camera. The LED board will enable us to define a specific set of LEDs as active, and these will start flashing based on randomized initial phase positions. The camera will serve as our sensor, capturing at a frame speed at least double of our LED flash frequency. In order to provide real-time adjustments to the LED's phases, the images will be processed in real-time LabVIEW and fed out by the LabVIEW digital output module to the LED board controller. This feedback loop will simulate the LED's "detecting" the surrounding flashes (through the camera) and phase-shifting according (through received digital output feedback).
This real-time image processing methodology allows for a convenient means of defining constraining conditions for our array of LEDs (e.g. which inter-LED "connections" are broken). Utilizing this experimental methodology, we will attempt to find the "breaking point" of LED synchrony for the following two simplified scenarios.
1) Given arrays of LEDs positioned as the vertices of different polygons, how many inter-LED connections can we break before global synchrony cannot be achieved consistently? We will impose the limitation that each LED, at most, will have only one of its connections broken.
2) For two equivalent sized families of LEDs where only one LED from each family can see each other, how large will the families need to be in order to consistently achieve local synchrony/stability such that they are unperturbed by the two inter-family LEDs? For a family, every LED included will be able to see every other LED within the same family.
Bibliography
Strogatz, S. H., Mirollo, R. E. Synchronization of Pulse-Coupled Biological Oscillators. SIAM Journal on Applied Mathematics. (50) 1645-1662.
Strogatz, S. H., Exploring Complex Networks. Nature (410) 268-276.
Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence (Springer, Berlin, 1984).
Winfree, A. T. The Geometry of Biological Time (Springer, New York, 1980).
Collins, J. J. & Stewart, I. Coupled nonlinear oscillators and the symmetries of animal gaits. J. Nonlin. Sci. 3, 349–392 (1993).