Group 2 2012: Difference between revisions
No edit summary |
No edit summary |
||
| Line 7: | Line 7: | ||
== Background == | == Background == | ||
The flashing of fireflies is a familiar biological phenomenon that has been studied for hundreds of years | The flashing of fireflies is a familiar biological phenomenon that has been studied for hundreds of years (Ermentrout, 1991). Its purpose is currently as a courtship behavior used during the mating season of the particular species, with usually mobile males flashing to signal typically stationary flashing females (Ermentrout, 1991). As is the case for many biological oscillators, it has been observed (Buck, 1938) that when a population of fireflies flash in response to each other, coupling their dynamics, the characteristically nonlinear phenomenon of synchrony can occur, with the fireflies all flashing with identical frequencies. | ||
<videoflash>a-Vy7NZTGos</videoflash> | <videoflash>a-Vy7NZTGos</videoflash> | ||
( | There exist numerous models for the scenario of a population of flashing and synchronizing fireflies. The first of such models is proposed by Strogatz (Mirollo, 1990): | ||
Consider the scenario of a population of oscillators, each with identical parameters in amplitude and frequency, only distinguished by the their offset phases. Now, introduce another constraint, establishing that each oscillator is coupled equally to all others, regardless of their relative proximity. Under such conditions, global synchronization of the oscillators has a high probability of being achieved (Strogatz, Nature). This model can be applied to firefly synchronization, so long as the model caveats are satisfied. Specifically, the fireflies are assumed to be identical, have perfect line-of-sight of every other firefly, and are equally perturbed by nearby and distant flashes. | |||
For our study, we adopted many of the assumptions described in the Strogatz model, namely that every firefly within our system had identical state dynamics and followed the same intrinsic frequency. However, we opted for a more biological-motivated model derived from the Kuramoto model (of our own design), as well as a line-of-sight scheme that gave our model a spatial representation that is not often found in the modeling of nonlinear oscillator synchronization. | |||
== Updated Kuramoto Model == | == Updated Kuramoto Model == | ||
| Line 25: | Line 25: | ||
$$\displaystyle{d\theta_{i}\over{dt}} = \omega_t + {K\over{N}}\sum\limits_{j \in \text{fired}} \sin(\theta_j - \theta_i)$$ | $$\displaystyle{d\theta_{i}\over{dt}} = \omega_t + {K\over{N}}\sum\limits_{j \in \text{fired}} \sin(\theta_j - \theta_i)$$ | ||
As an explanation as to why biologically realizable models, such as the updated Kuramoto equation, lead to synchronization, Strogatz | As an explanation as to why biologically realizable models, such as the updated Kuramoto equation, lead to synchronization, Strogatz (Mirollo, 1990) proposed the following set of criteria that guarantees two coupled oscillators will always synchronize: | ||
(i) $\displaystyle{d\phi \over{dt}} = {1\over{T}}$ models the change of phase of the oscillator | (i) $\displaystyle{d\phi \over{dt}} = {1\over{T}}$ models the change of phase of the oscillator | ||
| Line 39: | Line 39: | ||
(vi) When the state of the oscillator reaches the end of its interval, $2\pi$ or $1.0$ when normalized, it is reset to $0$ and perturbs the other oscillator by an amount, $\epsilon$, s.t. $\epsilon \in \mathbb{R}, \epsilon > 0$. | (vi) When the state of the oscillator reaches the end of its interval, $2\pi$ or $1.0$ when normalized, it is reset to $0$ and perturbs the other oscillator by an amount, $\epsilon$, s.t. $\epsilon \in \mathbb{R}, \epsilon > 0$. | ||
Figure 1 details the listed criteria. The internal state of the system, $x$, represents the nonlinear internal functioning of the oscillator. In fireflies, this would correspond to the nonlinear firings of the neurons. We can therefore state the following theorem | Figure 1 details the listed criteria. The internal state of the system, $x$, represents the nonlinear internal functioning of the oscillator. In fireflies, this would correspond to the nonlinear firings of the neurons. We can therefore state the following theorem (Mirollo, 1990): | ||
[[File:typicalf.png|thumb|center |1000px|alt=text|Figure 1: State variable, $x$, as a function of phase, $\phi$. Note the axes have been normalized by dividing by $2\pi$. (Strogatz, SIAM)]] | [[File:typicalf.png|thumb|center |1000px|alt=text|Figure 1: State variable, $x$, as a function of phase, $\phi$. Note the axes have been normalized by dividing by $2\pi$. (Strogatz, SIAM)]] | ||
| Line 182: | Line 182: | ||
Collins, J. J. & Stewart, I. Coupled nonlinear oscillators and the symmetries of animal gaits. J. Nonlin. | Collins, J. J. & Stewart, I. Coupled nonlinear oscillators and the symmetries of animal gaits. J. Nonlin. | ||
Sci. 3, 349–392 (1993). | Sci. 3, 349–392 (1993). | ||
Ermentrout, Bard. "An adaptive model for synchrony in the firefly pteroptyx malaccae." Journal of Mathematical Biology 29.6 (1991): 571-585. | |||
Buck, John Bonner. "Synchronous rhythmic flashing of fireflies." The Quarterly Review of Biology 13.3 (1938): 301-314. | |||
Revision as of 10:57, 14 December 2012
The Effects of Connection Topology on Synchronization Time in a Population of Fireflies
Group members: Ben McInroe, William Wagstaff, Mark Kingsbury, Morris Huang
Abstract
Firefly synchronization is a well-studied phenomena in nature that amends itself to models based on coupled oscillators. While many of these models have been mathematically proven to synchronize in the two oscillator case, and even the globally coupled case, it is not well understood whether groups of coupled oscillators synchronize if the topological connections between them are changed from global to local. In terms of fireflies, the fact that many fireflies remain grouped in trees or around bodies of water may be necessitated given the actual dynamics by which fireflies alter their internal frequencies. Our experimental results confirm this hypothesis by highlighting the ability of coupled oscillators to become saturated with information. By this, we mean that after a particular threshold of connections between fireflies, any additional connections do not reduce the time to synchronization. For fireflies, this means that the grouping behavior may be beneficial up to a critical point after which additional fireflies no longer aid in synchronization.
Background
The flashing of fireflies is a familiar biological phenomenon that has been studied for hundreds of years (Ermentrout, 1991). Its purpose is currently as a courtship behavior used during the mating season of the particular species, with usually mobile males flashing to signal typically stationary flashing females (Ermentrout, 1991). As is the case for many biological oscillators, it has been observed (Buck, 1938) that when a population of fireflies flash in response to each other, coupling their dynamics, the characteristically nonlinear phenomenon of synchrony can occur, with the fireflies all flashing with identical frequencies.
<videoflash>a-Vy7NZTGos</videoflash>
There exist numerous models for the scenario of a population of flashing and synchronizing fireflies. The first of such models is proposed by Strogatz (Mirollo, 1990):
Consider the scenario of a population of oscillators, each with identical parameters in amplitude and frequency, only distinguished by the their offset phases. Now, introduce another constraint, establishing that each oscillator is coupled equally to all others, regardless of their relative proximity. Under such conditions, global synchronization of the oscillators has a high probability of being achieved (Strogatz, Nature). This model can be applied to firefly synchronization, so long as the model caveats are satisfied. Specifically, the fireflies are assumed to be identical, have perfect line-of-sight of every other firefly, and are equally perturbed by nearby and distant flashes.
For our study, we adopted many of the assumptions described in the Strogatz model, namely that every firefly within our system had identical state dynamics and followed the same intrinsic frequency. However, we opted for a more biological-motivated model derived from the Kuramoto model (of our own design), as well as a line-of-sight scheme that gave our model a spatial representation that is not often found in the modeling of nonlinear oscillator synchronization.
Updated Kuramoto Model
We decided to use the Kuramoto model as a basis from which to investigate the synchronization of biological oscillators due to its simplicity. It makes no assumptions about the computational capacities of the firefly other than the ability of the firefly to recognize the strength of light that is emitted from its neighbors. The Kuramoto model can be described by the following equation: $$\displaystyle{d\theta_{i}\over{dt}} = \omega_t + {K\over{N}}\sum\limits_{j = 1}^{N} \sin(\theta_j - \theta_i)$$
Here, $\theta$ is the phase of the oscillator, $K$ is the coupling constant, and $N$ is the number of oscillators. One problem with this model is that it assumes that the oscillators know the instantaneous phase of all other oscillators for all time. Therefore, we propose an updated form of the model that incorporates the biological constraints of discrete communication described above: $$\displaystyle{d\theta_{i}\over{dt}} = \omega_t + {K\over{N}}\sum\limits_{j \in \text{fired}} \sin(\theta_j - \theta_i)$$
As an explanation as to why biologically realizable models, such as the updated Kuramoto equation, lead to synchronization, Strogatz (Mirollo, 1990) proposed the following set of criteria that guarantees two coupled oscillators will always synchronize:
(i) $\displaystyle{d\phi \over{dt}} = {1\over{T}}$ models the change of phase of the oscillator
(ii) $\phi = 0$ when the oscillator is at its lowest state $x = 0$
(iii) $\phi = 2\pi$ when the oscillator reaches threshold at $x = 2\pi$
(iv) $x = f(\phi)$ maps the phase of the oscillator to its internal state variable x. $f$ is smooth, monotonically increasing, and concave down, i.e. $f' > 0, f < 0$
(v) $f$ is invertible such that $g = f^{-1}$, where g is monotonically increasing and concave up, i.e. $g' > 0$ and $g > 0$
(vi) When the state of the oscillator reaches the end of its interval, $2\pi$ or $1.0$ when normalized, it is reset to $0$ and perturbs the other oscillator by an amount, $\epsilon$, s.t. $\epsilon \in \mathbb{R}, \epsilon > 0$.
Figure 1 details the listed criteria. The internal state of the system, $x$, represents the nonlinear internal functioning of the oscillator. In fireflies, this would correspond to the nonlinear firings of the neurons. We can therefore state the following theorem (Mirollo, 1990):
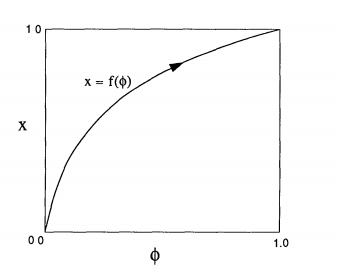
Theorem 1: Any two oscillators that satisfy conditions (i) through (vi) will always become synchronized.
While this Theorem provides a standard criteria that guarantees synchronization, it is by no means all encompassing as it does not account for periodic perturbations, $\epsilon$, or linear phase curves, $f$, that accompany the updated Kuramoto model. We, therefore, propose the following additional criteria:
(i) $\displaystyle{d\phi \over{dt}} = {\omega}$ models the change of phase of the oscillator
(ii) $\phi = 0$ when the oscillator is at its lowest state $x = 0$
(iii) $\phi = 2\pi$ when the oscillator reaches threshold at $x = 2\pi$
(iv) $x = f(\phi)$ maps the phase of the oscillator to its internal state variable $x$
(v) $f$ is invertible such that $g = f^{-1}$
(vi) $g = f$ such that $g$ and $f$ are the identity functions, $g(x) = f(\phi) = Id(x) = Id(\phi)$, which implies that $x = \phi$
(vii) When the state of the oscillator A reaches the end of its interval, $2\pi$, A is reset to $0$ and perturbs the other oscillator, B, by an amount, $\epsilon = \sin(\phi)$
(viii) Oscillators A and B have initial phases that differ by $|\phi_A-\phi_B| \ne \pi$
Therefore, we have the new scenario in Figure 2, which is the case where $f$ is a linear function, and $\epsilon$ is a periodic perturbation that depends on the position of the oscillators in phase space.
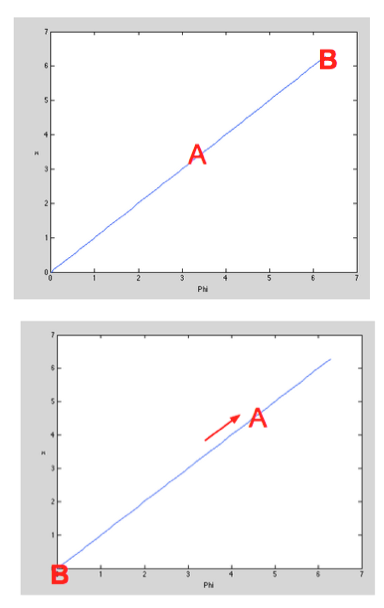
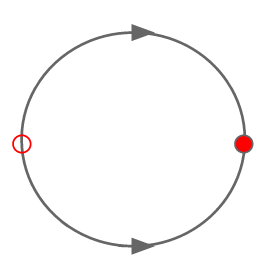
It helps to think of oscillators A and B moving around the unit circle (Figure 4).

Theorem 2: Any two oscillators that satisfy conditions (i) through (viii) will always become synchronized.
Proof
To prove that this scenario leads to synchronization, we need to define a return map $R(\phi)$ for the phase of B immediately after the next firing of A. Take two oscillators A and B initially at position $(0, \phi)$, such that B is about to fire (Figure 3). After a time $2\pi - \phi$, B fires (Figure 4), at which point B returns to 0 and A is at a point, $2\pi - \phi + \sin(\phi)$, where $\sin(\phi)$ is the perturbation made upon A by B's firing.
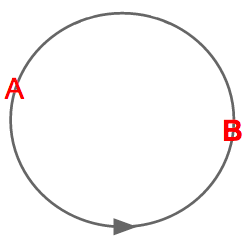
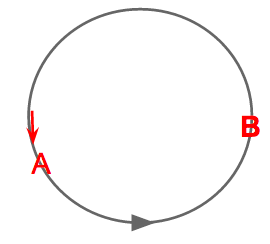
Now we define the firing map $h : \phi \mapsto \phi $ by: $$h(\phi) = 2\pi -\phi + \sin(\phi)$$
Therefore, the new positions of A and B are: $$(\phi_A,\ \phi_B) = (h(\phi), 0)$$
We assume $0<h(\phi)<2\pi$, otherwise the fireflies will have synchronized (thus completing the proof). This implies $\phi: (0,2\pi)$
Due to the symmetry of the oscillators, after A fires and is reset to 0, the positions of A and B are found by iterating the firing map once more giving: $$(\phi_A, \phi_B) = (0, h(h(\phi)))$$
We can therefore define the return map as: $$R(\phi) = h(h(\phi)) = \phi-\sin(\phi)-\sin(\phi-\sin(\phi))$$
To investigate the stability of the fixed map, we must calculate its fixed points. We note that that fixed points of $h$ are also fixed points of $R$. Therefore, $R$ has fixed points when: $h(\phi) = \phi = 2\pi - \phi + \sin(\phi) \phi ^* = 0, \pi$
Now we can investigate the stability of the fixed points by looking at the derivative of the return map: $R'(\phi) = (\cos(\phi)-1) (\cos(\phi-\sin(\phi))-1)$
Plugging in the fixed points we find: $R'(0) = 0 < 1$ (Stable) $R'(\pi) = 4 > 1$ (Unstable)
Therefore, the two coupled oscillators always synchronize so long as their phase difference does not differ by exactly $\pi$. In this case, the oscillators remained entrained and differ in phase by $\pi$ for all time. The stability of the system is presented in Figure 5. $\Box$
Additional Conditions
Suppose instead that $\epsilon = K\sin(\phi)$ where $K \in \mathbb{R}$. We take $K \ge 0$ since $-K\sin(\phi) = K\sin(-\phi)$. This corresponds to a scaling of the perturbation made by the firing oscillator on the non firing oscillator. In this case, the firing map becomes: $$\displaystyle h(\phi) = 2\pi-\phi +K\sin(\phi)$$
And our return map becomes: $$\displaystyle R(\theta) = -K\sin(\phi)-K\sin(\phi-K\sin(\phi))+ \phi $$
Like before, we need to calculate the fixed points of the system by letting $R(\phi) = \phi$, which is equivalent to: $$\displaystyle \sin(\phi)+\sin(\phi-K\sin(\phi)) = 0 \equiv \sin \phi = {2 \phi\over{K}}$$
Bifurcation Analysis
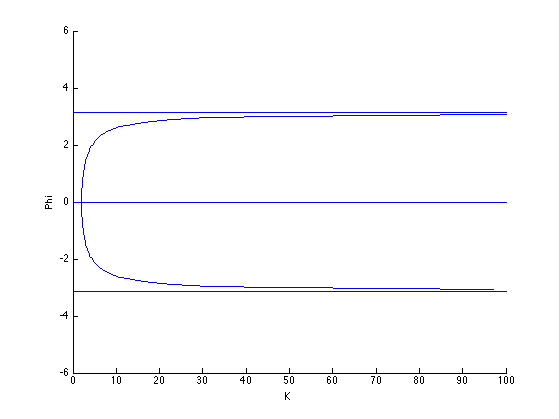
This firing map has fixed points $\phi^* = 0,\pi$ for all time; however, by graphing the bifurcation diagram ($\displaystyle K = {2\phi\over{\sin(\phi)}}$ flipped across the line $y=x$) we see some interesting behavior (Figure 6).
We first take the derivative of $R(\phi)$ at $\phi = 0$ and at $\phi = \pi$:
$\displaystyle R'(0) = (K-1)^2 $ $\displaystyle R'(\pi) = (K+1)^2 $
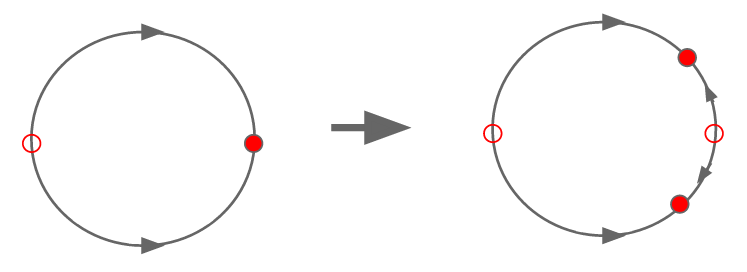
We immediately notice that for $K>0, R'(\pi) > 1$; for $K > 2, R'(0) > 1$; and for $0 < K \le 2, R'(0) < 1$. This means that for $0 < K \le 2$, $0$ is a stable node, and $\pi$ is an unstable node; however, when $K > 2$, $0$ swaps to an unstable node. Therefore, at $K = 2$, the system undergoes a supercritical pitchfork bifurcation leading to the birth of two new stable nodes (Figure 7).
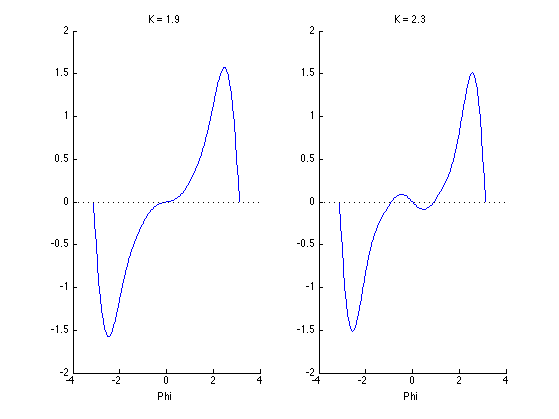
We can see this clearly in graphs of $R(\phi) = \phi$ for increasing values of $K$ (Figure 8).
The two new stable nodes are born from the node at $0$ and move towards the node at $\pi$ becoming arbitrarily close to $\pi,-\pi$ as $K \rightarrow \infty$. Therefore, synchronization will occur when $0 < K \le 2$; however, when $K > 2$, it is possible for the oscillators to become synchronized if they begin synchronized; however, it is more likely they will become entrained at the new stable fixed points.
It is important to note that Theorem 2 justifies using the Kuramoto model in the biologically realistic case in which coupled oscillators perturb each other in discrete time. We can additionally focus on altering the coupling topologies without worry that the model itself is causing a lack of synchronization. Furthermore, the K values used in the experiments never exceed this bifurcation level.
Experiment
Our experimental setup consisted of a 6 by 8 grid of LEDs soldered onto a pre-made Peggy2 LED board. The board was controlled by a microcontroller based on the Arduino platform, which in turn was controlled by MATLAB. The board was monitered by a webcam that collected images, and then sent them to a MATLAB image processing program. A set of different values for the coupling constant, K, and connection matrix, $A_{ij}$ were tested, with each pair of coupling constant and connection matrix being run over 15 trials with randomized initial conditions. The choices of $A_{ij}$ and K are summarized below.
Matrix A (for the following line-of-sight radii | number of connections per firefly)
R = 1 | C = 4
R = sqrt(2) | C = 8
R = 2 | C = 12
R = sqrt(5) | C = 20
R = 3 | C = 27
R = sqrt(13) | C = 33
R = 4 | C = 40
R = sqrt(20) | C = 46
R = 5 | C = 47
Coupling Strengths
K = 1, 2, 5, 7, 10, 15, 20, 25
Below is a video of a synchronization trial at R = 1 (nearest neighbors in the 4 cardinal directions), K = 15.
<videoflash>PZ4_o-e8GdE</videoflash>
Conclusion
Our project will examine how global synchronization breaking can occur in disjoint populations of oscillating fireflies through experimental means. It will be achieved by simulating networks of fireflies as LED lights in a network with physical boundaries and oscillator phase determined through the use of our high speed camera and computer program. Through these methods, we hope to better understand how variations in the network geometry of firefly populations can affect their ability to mutually synchronize.
Bibliography
Strogatz, S. H., Mirollo, R. E. Synchronization of Pulse-Coupled Biological Oscillators. SIAM Journal on Applied Mathematics. (50) 1645-1662.
Strogatz, S. H., Exploring Complex Networks. Nature (410) 268-276.
Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence (Springer, Berlin, 1984).
Winfree, A. T. The Geometry of Biological Time (Springer, New York, 1980).
Collins, J. J. & Stewart, I. Coupled nonlinear oscillators and the symmetries of animal gaits. J. Nonlin. Sci. 3, 349–392 (1993).
Ermentrout, Bard. "An adaptive model for synchrony in the firefly pteroptyx malaccae." Journal of Mathematical Biology 29.6 (1991): 571-585.
Buck, John Bonner. "Synchronous rhythmic flashing of fireflies." The Quarterly Review of Biology 13.3 (1938): 301-314.