Group 2 2012: Difference between revisions
| Line 153: | Line 153: | ||
Here, $A_{i,j}$ is the coupling matrix such that $A_{i,j} = 1$ if there exists and connection between firefly $i$ and firefly $j$. In physical terms, if firefly $i$ can see firefly $j$, then $A_{i,j}=1$, otherwise $A_{i,j}=0$. | Here, $A_{i,j}$ is the coupling matrix such that $A_{i,j} = 1$ if there exists and connection between firefly $i$ and firefly $j$. In physical terms, if firefly $i$ can see firefly $j$, then $A_{i,j}=1$, otherwise $A_{i,j}=0$. | ||
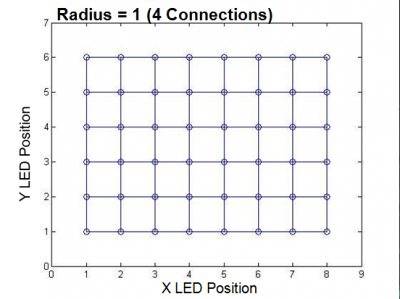
The LED board is an 6x8 grid with 48 fireflies. We adjust the line of sights for each firefly by altering the connection matrix. For example, Figure 10 details a line of sight radius of 1; therefore, each firefly can only see its four neighbors in each of the cardinal directions. Figure 11 details a line of sight radius of $\sqrt{2}$, which corresponds to a firefly seeing all 8 of its adjacent neighbors. | |||
For all experiments, we assume that the board is on a torus; that is, fireflies across the top row can see fireflies on the bottom, fireflies on the left can see fireflies on the right, and vice versa. This constraint avoids the cases when oscillations bunch up around the corners; these scenarios lead to synchronization times that are highly dependent on start condition | |||
All the experiments were performed in the following manner: the radius is selected and fixed, while the coupling constant $K$ is varied. At each start, the phases of all 48 fireflies are uniformly distributed around the unit circle. Then, the model is run for 3000 iterations, where each iteration corresponds to a single $\theta$ update for every firefly. A single iteration is proportional to the time constant, $\tau$. We performed this experiment 10 times for each $K$ - radius pair given in the table below. | |||
R = 1 | C = 4 <br /> | R = 1 | C = 4 <br /> | ||
| Line 169: | Line 175: | ||
K = 1, 2, 5, 7, 10, 15, 20, 25 | K = 1, 2, 5, 7, 10, 15, 20, 25 | ||
<br /> <br /> | <br /> <br /> | ||
Below is a video of a synchronization trial at <br /> | Below is a video of a synchronization trial at <br /> | ||
Revision as of 11:25, 14 December 2012
The Effects of Connection Topology on Synchronization Time in a Population of Fireflies
Group members: Ben McInroe, William Wagstaff, Mark Kingsbury, Morris Huang
Abstract
Firefly synchronization is a well-studied phenomena in nature that amends itself to models based on coupled oscillators. While many of these models have been mathematically proven to synchronize in the two oscillator case, and even the globally coupled case, it is not well understood whether groups of coupled oscillators synchronize if the topological connections between them are changed from global to local. In terms of fireflies, the fact that many fireflies remain grouped in trees or around bodies of water may be necessitated given the actual dynamics by which fireflies alter their internal frequencies. Our experimental results confirm this hypothesis by highlighting the ability of coupled oscillators to become saturated with information. By this, we mean that after a particular threshold of connections between fireflies, any additional connections do not reduce the time to synchronization. For fireflies, this means that the grouping behavior may be beneficial up to a critical point after which additional fireflies no longer aid in synchronization.
Background
Synchronization in groups of fireflies plays a major role in reproduction, recognition, and competition (Avila, 2011). In reproduction, this communication regime consists of male fireflies flashing at a natural frequency with females responding accordingly. Because the response of the female requires coherency in the firings of the males, the male fireflies have developed methods of altering their internal frequency leading to synchronized flashing.
<videoflash>a-Vy7NZTGos</videoflash>
To explain this phenomenon, researchers have focused on the dynamics of coupled oscillators as a model for this synchronization behavior (Mirollo, 1990). In this paradigm, two entities influence each other's dynamics through a mutual exchange of information. For example, fireflies communicate their phase positions and frequencies with each flash. Implicit to the biology is the limitation that any firefly hoping to synchronize must either wait for or estimate the phase information of other fireflies. Therefore, any model of synchronization must account for these biological constraints by incorporating discrete forms of communication between the oscillators.
A number of models have been developed to account for this synchronization phenomenon and include such examples as the Kuramoto model for chemical oscillators (Acebron, 2005) along with Peskin's model for self-synchronization of cardiac pacemaker cells (Peskin, 1975). Both of these examples have been mathematically proven to synchronize in the two oscillator case, and have been experimentally shown to synchronize in the globally coupled case; however, it is not well understood whether groups of coupled oscillators will still synchronize if the topological connections between them are changed from global to local.
One particularly overlooked component of firefly synchronization is the topology of firefly groups in trees or around bodies of water \cite{Buck:1938wt}. While this seems necessary given the firefly's need to physically see its neighbors in order to synchronize, this grouping behavior may actually be necessitated by the dynamics by which fireflies alter their internal frequencies. For example, suppose one group of fireflies is on one side of a tree, another group is on the opposing side, and both are trying to communicate with one female in between. Because these groups are more likely to be unsynchronized, they are unlikely to warrant a response from the female given the lack of synchronization. Thus, it makes reproductive sense for these two groups to communicate with one another to some degree. In this paper, we hope to investigate the extent to which groups of fireflies communicate with one another.
We hypothesize that the ability of a firefly to synchronize quickly and successfully is directly proportional to the number of other fireflies that it can see.
Updated Kuramoto Model
We decided to use the Kuramoto model as a basis from which to investigate the synchronization of biological oscillators due to its simplicity. It makes no assumptions about the computational capacities of the firefly other than the ability of the firefly to recognize the strength of light that is emitted from its neighbors. The Kuramoto model can be described by the following equation: $$\displaystyle{d\theta_{i}\over{dt}} = \omega_t + {K\over{N}}\sum\limits_{j = 1}^{N} \sin(\theta_j - \theta_i)$$
Here, $\theta$ is the phase of the oscillator, $K$ is the coupling constant, and $N$ is the number of oscillators. One problem with this model is that it assumes that the oscillators know the instantaneous phase of all other oscillators for all time. Therefore, we propose an updated form of the model that incorporates the biological constraints of discrete communication described above: $$\displaystyle{d\theta_{i}\over{dt}} = \omega_t + {K\over{N}}\sum\limits_{j \in \text{fired}} \sin(\theta_j - \theta_i)$$
As an explanation as to why biologically realizable models, such as the updated Kuramoto equation, lead to synchronization, Strogatz (Mirollo, 1990) proposed the following set of criteria that guarantees two coupled oscillators will always synchronize:
(i) $\displaystyle{d\phi \over{dt}} = {1\over{T}}$ models the change of phase of the oscillator
(ii) $\phi = 0$ when the oscillator is at its lowest state $x = 0$
(iii) $\phi = 2\pi$ when the oscillator reaches threshold at $x = 2\pi$
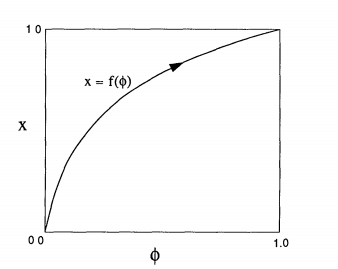
(iv) $x = f(\phi)$ maps the phase of the oscillator to its internal state variable x. $f$ is smooth, monotonically increasing, and concave down, i.e. $f' > 0, f < 0$
(v) $f$ is invertible such that $g = f^{-1}$, where g is monotonically increasing and concave up, i.e. $g' > 0$ and $g > 0$
(vi) When the state of the oscillator reaches the end of its interval, $2\pi$ or $1.0$ when normalized, it is reset to $0$ and perturbs the other oscillator by an amount, $\epsilon$, s.t. $\epsilon \in \mathbb{R}, \epsilon > 0$.
Figure 1 details the listed criteria. The internal state of the system, $x$, represents the nonlinear internal functioning of the oscillator. In fireflies, this would correspond to the nonlinear firings of the neurons. We can therefore state the following theorem (Mirollo, 1990):
Theorem 1: Any two oscillators that satisfy conditions (i) through (vi) will always become synchronized.
While this Theorem provides a standard criteria that guarantees synchronization, it is by no means all encompassing as it does not account for periodic perturbations, $\epsilon$, or linear phase curves, $f$, that accompany the updated Kuramoto model. We, therefore, propose the following additional criteria:
(i) $\displaystyle{d\phi \over{dt}} = {\omega}$ models the change of phase of the oscillator
(ii) $\phi = 0$ when the oscillator is at its lowest state $x = 0$
(iii) $\phi = 2\pi$ when the oscillator reaches threshold at $x = 2\pi$
(iv) $x = f(\phi)$ maps the phase of the oscillator to its internal state variable $x$
(v) $f$ is invertible such that $g = f^{-1}$
(vi) $g = f$ such that $g$ and $f$ are the identity functions, $g(x) = f(\phi) = Id(x) = Id(\phi)$, which implies that $x = \phi$
(vii) When the state of the oscillator A reaches the end of its interval, $2\pi$, A is reset to $0$ and perturbs the other oscillator, B, by an amount, $\epsilon = \sin(\phi)$
(viii) Oscillators A and B have initial phases that differ by $|\phi_A-\phi_B| \ne \pi$
Therefore, we have the new scenario in Figure 2, which is the case where $f$ is a linear function, and $\epsilon$ is a periodic perturbation that depends on the position of the oscillators in phase space.
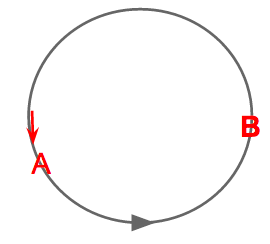
It helps to think of oscillators A and B moving around the unit circle (Figure 4).

Theorem 2: Any two oscillators that satisfy conditions (i) through (viii) will always become synchronized.
Proof
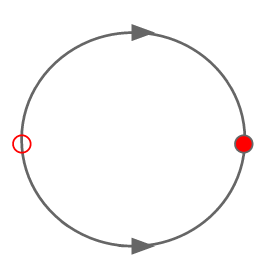
To prove that this scenario leads to synchronization, we need to define a return map $R(\phi)$ for the phase of B immediately after the next firing of A. Take two oscillators A and B initially at position $(0, \phi)$, such that B is about to fire (Figure 3). After a time $2\pi - \phi$, B fires (Figure 4), at which point B returns to 0 and A is at a point, $2\pi - \phi + \sin(\phi)$, where $\sin(\phi)$ is the perturbation made upon A by B's firing.
Now we define the firing map $h : \phi \mapsto \phi $ by: $$h(\phi) = 2\pi -\phi + \sin(\phi)$$
Therefore, the new positions of A and B are: $$(\phi_A,\ \phi_B) = (h(\phi), 0)$$
We assume $0<h(\phi)<2\pi$, otherwise the fireflies will have synchronized (thus completing the proof). This implies $\phi: (0,2\pi)$
Due to the symmetry of the oscillators, after A fires and is reset to 0, the positions of A and B are found by iterating the firing map once more giving: $$(\phi_A, \phi_B) = (0, h(h(\phi)))$$
We can therefore define the return map as: $$R(\phi) = h(h(\phi)) = \phi-\sin(\phi)-\sin(\phi-\sin(\phi))$$
To investigate the stability of the fixed map, we must calculate its fixed points. We note that that fixed points of $h$ are also fixed points of $R$. Therefore, $R$ has fixed points when: $h(\phi) = \phi = 2\pi - \phi + \sin(\phi) \phi ^* = 0, \pi$
Now we can investigate the stability of the fixed points by looking at the derivative of the return map: $R'(\phi) = (\cos(\phi)-1) (\cos(\phi-\sin(\phi))-1)$
Plugging in the fixed points we find: $R'(0) = 0 < 1$ (Stable) $R'(\pi) = 4 > 1$ (Unstable)
Therefore, the two coupled oscillators always synchronize so long as their phase difference does not differ by exactly $\pi$. In this case, the oscillators remained entrained and differ in phase by $\pi$ for all time. The stability of the system is presented in Figure 5. $\Box$
Additional Conditions
Suppose instead that $\epsilon = K\sin(\phi)$ where $K \in \mathbb{R}$. We take $K \ge 0$ since $-K\sin(\phi) = K\sin(-\phi)$. This corresponds to a scaling of the perturbation made by the firing oscillator on the non firing oscillator. In this case, the firing map becomes: $$\displaystyle h(\phi) = 2\pi-\phi +K\sin(\phi)$$
And our return map becomes: $$\displaystyle R(\theta) = -K\sin(\phi)-K\sin(\phi-K\sin(\phi))+ \phi $$
Like before, we need to calculate the fixed points of the system by letting $R(\phi) = \phi$, which is equivalent to: $$\displaystyle \sin(\phi)+\sin(\phi-K\sin(\phi)) = 0 \equiv \sin \phi = {2 \phi\over{K}}$$
Bifurcation Analysis
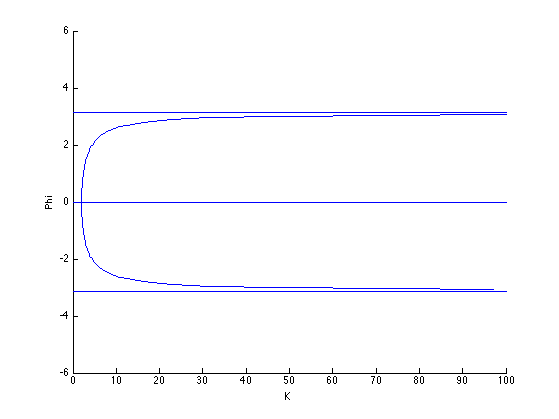
This firing map has fixed points $\phi^* = 0,\pi$ for all time; however, by graphing the bifurcation diagram ($\displaystyle K = {2\phi\over{\sin(\phi)}}$ flipped across the line $y=x$) we see some interesting behavior (Figure 6).
We first take the derivative of $R(\phi)$ at $\phi = 0$ and at $\phi = \pi$:
$\displaystyle R'(0) = (K-1)^2 $ $\displaystyle R'(\pi) = (K+1)^2 $
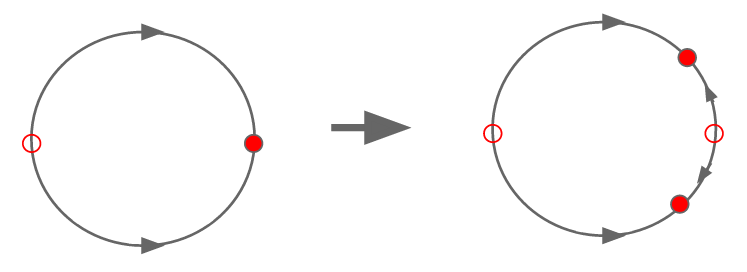
We immediately notice that for $K>0, R'(\pi) > 1$; for $K > 2, R'(0) > 1$; and for $0 < K \le 2, R'(0) < 1$. This means that for $0 < K \le 2$, $0$ is a stable node, and $\pi$ is an unstable node; however, when $K > 2$, $0$ swaps to an unstable node. Therefore, at $K = 2$, the system undergoes a supercritical pitchfork bifurcation leading to the birth of two new stable nodes (Figure 7).
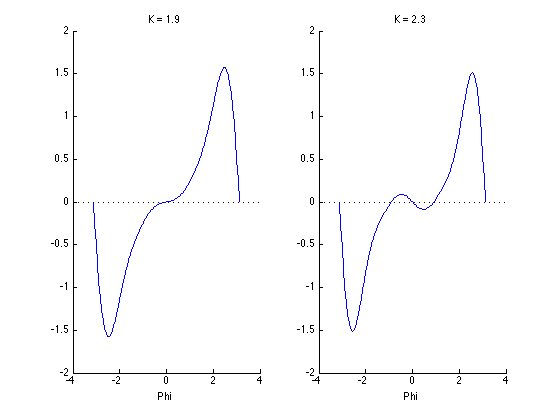
We can see this clearly in graphs of $R(\phi) = \phi$ for increasing values of $K$ (Figure 8).
The two new stable nodes are born from the node at $0$ and move towards the node at $\pi$ becoming arbitrarily close to $\pi,-\pi$ as $K \rightarrow \infty$. Therefore, synchronization will occur when $0 < K \le 2$; however, when $K > 2$, it is possible for the oscillators to become synchronized if they begin synchronized; however, it is more likely they will become entrained at the new stable fixed points.
It is important to note that Theorem 2 justifies using the Kuramoto model in the biologically realistic case in which coupled oscillators perturb each other in discrete time. We can additionally focus on altering the coupling topologies without worry that the model itself is causing a lack of synchronization. Furthermore, the K values used in the experiments never exceed this bifurcation level.
Experiment

To investigate the effect of firefly couplings on time and ability to synchronize, we designed a physical setup using a camera, an LED board, and Matlab (Figure 9). The camera takes images of the board at 30 FPS, and sends the data to Matlab. Matlab uses blob detection to determine the locations and statuses of the LEDs - whether on or off. Once the ON LEDs' locations are determined, the phases for all the fireflies that didn't fire are updated using the following equation:
$$\displaystyle{d\theta_{i}\over{dt}} = \omega_t + {K\over{N}}\sum\limits_{j \in \text{fired}} A_{i,j}\sin(\theta_j - \theta_i)$$ Here, $A_{i,j}$ is the coupling matrix such that $A_{i,j} = 1$ if there exists and connection between firefly $i$ and firefly $j$. In physical terms, if firefly $i$ can see firefly $j$, then $A_{i,j}=1$, otherwise $A_{i,j}=0$.
The LED board is an 6x8 grid with 48 fireflies. We adjust the line of sights for each firefly by altering the connection matrix. For example, Figure 10 details a line of sight radius of 1; therefore, each firefly can only see its four neighbors in each of the cardinal directions. Figure 11 details a line of sight radius of $\sqrt{2}$, which corresponds to a firefly seeing all 8 of its adjacent neighbors.
For all experiments, we assume that the board is on a torus; that is, fireflies across the top row can see fireflies on the bottom, fireflies on the left can see fireflies on the right, and vice versa. This constraint avoids the cases when oscillations bunch up around the corners; these scenarios lead to synchronization times that are highly dependent on start condition
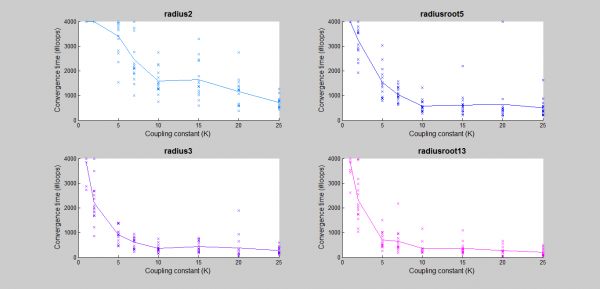
All the experiments were performed in the following manner: the radius is selected and fixed, while the coupling constant $K$ is varied. At each start, the phases of all 48 fireflies are uniformly distributed around the unit circle. Then, the model is run for 3000 iterations, where each iteration corresponds to a single $\theta$ update for every firefly. A single iteration is proportional to the time constant, $\tau$. We performed this experiment 10 times for each $K$ - radius pair given in the table below.
R = 1 | C = 4
R = sqrt(2) | C = 8
R = 2 | C = 12
R = sqrt(5) | C = 20
R = 3 | C = 27
R = sqrt(13) | C = 33
R = 4 | C = 40
R = sqrt(20) | C = 46
R = 5 | C = 47
Coupling Strengths
K = 1, 2, 5, 7, 10, 15, 20, 25
Below is a video of a synchronization trial at
R = 1 (nearest neighbors in the 4 cardinal directions), K = 15.
<videoflash>PZ4_o-e8GdE</videoflash>
Results
The data collected for each of the 1080 trials were the sum squared error between the internal phases of each individual firefly in the system, and the number of fireflies that had "fired" (aka LED's that lit up) for every loop iteration. This data was output as .mat files for convenience of analysis in Matlab.
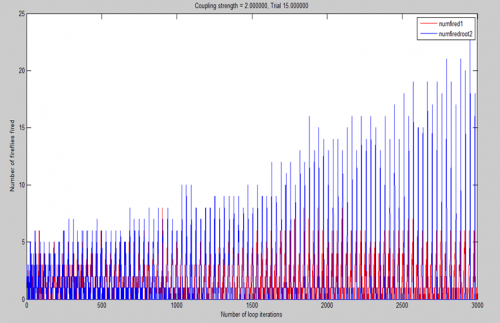
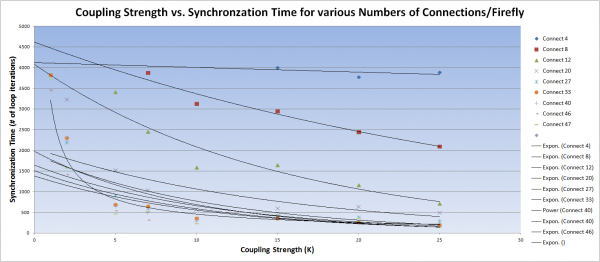
In the image to the right, the synchronization of fireflies given the same initial conditions but with different sight radii can be observed. The sight radius of 1.414 (8 connections/firefly) represented by the blue line appears to develop into a stable frequency as more and more fireflies are being entrained to fire simultaneously. Conversely, with the sight radius of 1 (4 connections/firefly), the red line does not appear to increase in number of fireflies fired simultaneously in a single frame/loop, and as a result, appears to have a less stable frequency. This outcome is logical, as one would expect as the number of connections/firefly increases, the synchronization time would decrease.
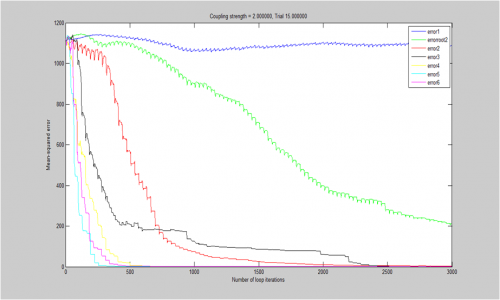
In the image to the left, we can again observe that the synchronization time for the system decreases as the sight radius decreases, where the synchronization time is defined as the loop iteration at which the sum squared error of the internal phases reaches 1, an error value at which the lights consistently appear to be flashing in synchrony to the human eye. This plot is part of pilot data an is meant to illustrate the error metric used per trial to define system synchronization. Note also the inverse relationship between the sum squared error of the internal phases and the peak number of fireflies firing in the same frame (in synchrony).
Conclusion
We initially hypothesized that fireflies group up around common environmental hotspots in order to improve their ability to communicate phase information. Our experimental results confirm this hypothesis by highlighting the ability of coupled oscillators to synchronize more quickly with more information; however, after a critical point, the fireflies become saturated with information. By this, we mean that after a particular threshold of connections between fireflies, any additional connections do not reduce the time to synchronization.
For fireflies, this means that the grouping behavior may be beneficial up to a critical point after which additional fireflies no longer aid in synchronization.; therefore, we hypothesize that fireflies receiving limited amounts of phase information will seek out other groups of fireflies in order improve its ability to synchronize. We hope to investigate this in future work.
Bibliography
Acebrón, J. A., Bonilla, L. L., Vicente, C., & Ritort, F. (2005). The Kuramoto model: A simple paradigm for synchronization phenomena. Reviews of Modern ….
Ávila, G., Deneubourg, J. L., & Guisset, J. L. (2011). Firefly courtship as the basis of the synchronization-response principle. EPL (Europhysics)
Buck, John Bonner. "Synchronous rhythmic flashing of fireflies." The Quarterly Review of Biology 13.3 (1938): 301-314.
Collins, J. J. & Stewart, I. Coupled nonlinear oscillators and the symmetries of animal gaits. J. Nonlin. Sci. 3, 349–392 (1993).
Ermentrout, Bard. "An adaptive model for synchrony in the firefly pteroptyx malaccae." Journal of Mathematical Biology 29.6 (1991): 571-585.
Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence (Springer, Berlin, 1984).
Strogatz, S. H., Mirollo, R. E. Synchronization of Pulse-Coupled Biological Oscillators. SIAM Journal on Applied Mathematics. (50) 1645-1662.
Strogatz, S. H., Exploring Complex Networks. Nature (410) 268-276.
Winfree, A. T. The Geometry of Biological Time (Springer, New York, 1980).